
Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
Declaración:
La mayoría de ejercicios de este post, proceden de las olimpíadas matemáticas aplicadas en México, como también de las realizadas por el maestro Mate, C.E.O. de este proyecto. A fin de coadyuvar en las soluciones se ha mantenido al máximo el enunciado general. La modalidad de solución de cada problema nos pertenece, pero la compartimos con mucho gusto.
Problema Nº 1
El doble del producto de las edades enteras de un padre y su hijo es 2006. Entonces, cuando el hijo nació la edad del padre era:
Solución
Sean h y p las edades del hijo y el padre, por tanto
2*h*p=2006
h=1003/p (h & p deben ser enteros)
El único entero que devuelve 1003/p a su vez un entero es p=59, y por tanto h =17
El padre tenía 59-17 = 42 años cuando nació el hijo.
Problema Nº 2
Desde una ciudad A parten trenes hacia la ciudad B. Por otro
lado, desde B parte un tren hacia A cada hora a la hora exacta. En ambos
casos el viaje dura 3 horas 45 minutos. Si Carlos toma el tren de A a B a las 12 en punto del mediodía, ¿cuántos trenes procedentes de B, Carlos, ve pasar durante el viaje?
Solución:
Debe tomar en cuenta a los trenes que salieron de B, antes que Carlos parta, y que aún no han llegado y luego los que salieron, de B, a las 12,13,14, y 15
Ve pasar 7.
Problema Nº 3
Si a + b + c = 0 entonces ¿a qué es igual a3+b3+c3?
Como a+b+c=0 entonces (a+b+c)3 =03 = 0
Además
(a+b+c)3 = a3+b3+c3 +3(a2b+a2c+b2a+b2c+c2a+c2b)+6abc
por tanto
por tanto
0 = a3+b3+c3 +3[a2(b+c) +b2(a+c)+c2(a+b)] +6abc
Como a+b+c=0 ==> b+c=-a
Como a+b+c=0 ==> b+c=-a
a+c=-b
a+b=-c
0 = a3+b3+c3 +3[a2(-a) +b2(-b)+c2(-c)] +6abc
0 = a3+b3+c3 +3(-a3-b3-c3) +6abc
0 = a3+b3+c3 -3(a3+b3+c3) +6abc
0 =-2(a3+b3+c3) +6abc
2(a3+b3+c3 ) =6abc
a3+b3+c3 =3abc
a3+b3+c3 =3abc
Problema Nº 4
Considere el triángulo ABC donde AB es el diámetro de una circunferencia, C se encuentra en la circunferencia y CD es la altura del triángulo desde el vértice C. Si el segmento AD = 25 cm y el segmento DB = 16 cm, hallar el área del triángulo ABC.
Solución #1:
Tomando el punto A como origen de coordenadas, la ecuación de la circunferencia es:
(x-20.5)2+y2=(20.52)2 (El radio es = (25+16)/2)
Si x = 25 entonces
4.52 +Y2 = 20.52
Si x = 25 entonces
4.52 +Y2 = 20.52
Y2=20.52 – 4.52
Y2=400
Y2=202
Y=20 (altura del triángulo)
Área= 41*20/2=410
Solución # 2:
Área= 41*20/2=410
Solución # 2:
Se descompone 25 en 20.5 y 4.5 y se forma el triángulo equilátero de hipotenusa igual al radio 20.5
h2=20.52 – 4.52
h2= 4002
h=20
Área = (25+16)*20/2 = 410
Problema Nº 5 h2= 4002
h=20
Área = (25+16)*20/2 = 410
Se utilizan cada uno de los cuatro dígitos 1, 9, 8 y 6 una y sólo una vez para formar dos números, de una, dos o tres cifras. ¿Cuál es el mayor valor posible del producto de números así formados?
Solución 1:
Caso 1
Un número de una cifra y uno de tres cifras
De una cifra =a
De tres cifras= bcd = b*100+c*10+d
El producto es: (b*100+c*10+d)*a=ab100+ac10+ad
ab debe ser máximo entonces a=9 & b=8
ac debe ser máximo c debe ser 6
d no tiene más alernativa que ser 1
y los números son: 861 & 9 ==> que el producto es 7749
Caso2
Dos números de dos cifras
Primer número = ab = 10a+b
Segundo número = cd = 10c +d
El producto es (10a+b)*(10c+d)= 100ac+10ad+10bc+db
= 100ac +10(ad+bc)+db
ac debe ser máximo ==> a=9 & c=8
ad+bc deben ser máximos==> d & b máximos ==> d=6 b =1 o d =1 & b=6
db debe ser máximo ==> d=6 & b=1
Por tanto la solución es
Primer número=91
Segundo número=86 y cuyo producto es 7826
Solución 2:
El producto de dos números es mayor, cuando menor es su diferencia, por lo que los números son 91 & 86 cuya diferencia es 5.
Problema Nº 6
Sea ABCD un trapecio isósceles el cual tiene lados de longitud AD = BC = 5, AB = 4 y DC = 10. El punto C está en el segmento DF y B es el punto medio de la hipotenusa DE del triangulo rectángulo DEF, entonces ¿cíal es la longitud del segmento CF?
Solución:
Altura del trapecio es:
h2=52-32
h=4
Por tanto EF =8
Cálculo de la longitud del segmento DB
(DB)2= 72+42= 65
DE=2*DB=2*SQRT(65)
Cálculo del segmento DF
(DF)2 = (DE)2 - (EF)2 = 4*65-64=196
DF = SQRT(196) = 14
CF = DF-DC =14-10
CF= 4
Problema Nº 7
El maestro pide a Carlos que copie en el pizarrón una tabla de dos columnas de números: En la primera columna, debe colocar, los múltiplos de 3 menores que 100, y en la segunda, sus correspondientes cuadrados. En un momento dado, Carlos escribe el número pero invirtiendo las cifras (unidades a la izquierda, luego decenas y luego centenas) lo mismo con el cuadrado. Para sorpresa suya, obtiene números idénticos a los escritos tres líneas más arriba. ¿Cuál es el número que Carlos debió escribir?
Solución:
El número 27 puede escribirse como 2*10 + 7 = 20 + 7=27
Sea cd el número que debía escribir, pero que escribió dc, por tanto las ecuaciones asociadas al enunciado son:
(1) Tres líneas más arriba, implica que la diferencia entre los números es 9.
(2) c + d debe se múltiplo de 3 (puesto que el ejercicio así lo plantea)
(3) c*10 + d -9 = d*10 + c ==> 9c=9d+9 ==> c=d+1 ==> d=c-1
c d
2 1
4 5
7 8 Entonces 21, 45 y 78 son los posibles números que Carlos debió escribir
Prueba
número cuadrado invertido cuadrado
21 441 12 144 (Solución)
45 2015 54 2916
78 6084 87 7569
Problema Nº 8
Juan miente siempre en martes, jueves y sábados y el resto de los días de la semana dice siempre la verdad. Si un día en particular, la conversación es la siguiente:
Pregunta: ¿Qué día es hoy?
Respuesta: Sábado.
Pregunta: ¿Qué día será mañana?
Respuesta: Miércoles.
¿De qué día de la semana se trata?
Solución:
Lunes
Martes
Miércoles
Jueves
Viernes
Sábado
Domingo
Caso 1:
Martes
Dice una mentira y una verdad (Mañana será miércoles), por tanto no puede ser martes.
Caso 2:
Sábado
No puede ser ya que diría una verdad (hoy es sábado)
Caso 3:
Jueves
Todas son mentiras
Por tanto la respuesta es Jueves.
Problema Nº 9
Si a · b = 12, b · c = 20, a · c = 15 y a es positivo, ¿cuánto vale a · b · c?
Solución:
Dividiendo
a.b=12
b.c=20 ==>a=(12/20)c
como
a.c=15 ==> (12/20)c*c=15 ==> c*c=25 ==> c=5
Finalmente
a=3
b=4
Por tanto a.b.c = 3*4*5=60
Solución alterna:
a.b*b.c*a.c = 12*20*15=
a2*b2*c2 =
(a*b*c)2 = 3600
(a*b*c)2 = 602 ==> a.b.c. = 60
Problema Nº 10
Dos misiles se desplazan en una misma línea de tal forma que chocarán en algún punto. Uno viaja a 2000 km/hora el otro a 1000 km/hora. ¿A qué distancia se encuentran un minuto antes del impacto?
Solución:
La velocidad 2000km/hora = 2000km/60 minutos
d1=2000*1/60
d2=1000*1/60
d =(2000+1000)/60=3000/60=50km
Si el área de una corona circular (región sombreada) es 25(PI)/2 cm2 ,
¿Cuál es la longitud de la cuerda PQ de la circunferencia mayor tangente a la menor?
Solución:
Área
sombreada=Área círculo externo - área del círculo interno
= (PI)r22 – (PI)r12
25(PI)/2 = (PI)(r22 – r12) ==> (r22 – r12) = 25/2
Cálculo de la cuerda
(PQ/2)2=r22-r12
Problema Nº 18
Un entero es tartamudo si todas sus cifras son iguales a 1.
¿Cuántos enteros positivos menores que 10,000,000 cumplen que al multiplicarlos por 33 se obtiene un entero tartamudo?
Solución
Los posibles números son:
La velocidad será n/60 para el valor entero de n que (1+2+3+..+n)/60 = 1 k recorrido entonces.
Como 1+2+3+..+n = n(n+1)/2=60 ==> n(n+1)=120 ==> n toma valores entre [10,11], y con n = 11 se garantiza el recorrido de 1000 m o 1 kilómetro
Velocidad es 11km/hora
Problema Nº 20
¿Cuál es el valor de b − a en la siguiente figura?
Solución:
Problema Nº 21
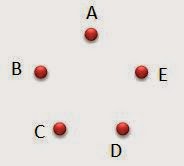
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los cinco puntos dados?
Problema Nº 22
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los siete puntos dados?
Problema Nº 24
Solución:
102
La centena del 100 tiene 19 números.
La centena del 200 tiene 100
La centena del 300 tiene 19
Solución: 138
Problema Nº 25
Un piso cuadriculado está cubierto por azulejos cuadrados del mismo tamaño de forma que quedan alineados. Los azulejos de las dos diagonales del piso son negros. Los azulejos restantes son blancos. Si hay 101 azulejos negros, ¿cuál es el número de azulejos blancos?
Solución:
PQ = 2*SQRT(r22-r12)
PQ= 2*SQRT(25/2) = 5*SQRT(2)
Problema Nº 12
Las bisectrices de los ángulos en A y en B en la base superior de un trapecio se cortan en el punto R. La razón entre la medida del ángulo agudo en R y la suma de las medidas de los ángulos en C y D de la base inferior es:
Solución:
Problema Nº 13
Las bisectrices de los ángulos en A y en B en la base superior de un trapecio se cortan en el punto R. La razón entre la medida del ángulo agudo en R y la suma de las medidas de los ángulos en C y D de la base inferior es:
Solución:
<R
= 180-µ-Ø
ε+¢ = 360-2µ-2Ø=2(180-µ-Ø)
<R/(ε+¢)
= ½
Dada la función f(n)=SQRT[1+(n2+n)(n+2)(n+3)], obtener una tabla para las duplas (n,f(n)) y luego una fórmula para el siguiente término de la sucesión f(n).
Solución:
Dados los términos 5, 11, 19, 29, 41, 55, ... se calculan las diferencias
6 8 10 12 14
6 8 10 12 14
y se calcula el enésimo térmimo:
Problema Nº 14
Problema Nº 14
Dada
la expresión 1 + (n2
+ n)(n2 + 5n + 6) = 2092, donde n es un número entero,
hallar valor de n(n + 3).
Nota: Debe ayudarse con el ejercicio anterior.
Solución:
Se observa que n es 13 y por tanto n(n+3)= 13*16
Problema Nº 15
Problema Nº 16
Cada arista de un cubo es coloreada roja o negra. Cada cara del cubo tiene al menos una arista negra. ¿Cuál es la menor cantidad de aristas negras que puede haber?
Un
niño
tiene tantas hermanas como hermanos, pero cada hermana tiene
tantas hermanas como la mitad de hermanos. ¿Cuántos hermanos y hermanas
hay
en la familia?
Solución:
Sean h los hermanos y m las hermanas
h-1=m (El niño tiene tantas hermanas como hemanos)
m-1=h/2==> (h-1)-1=h/2 (cada hermana tiene la mitad de hermanos)
h-2=h/2==>h/2=2==>h=4
m=h-1=4-1=3
Hay 4 hermanos y 7 hermanas
Cada arista de un cubo es coloreada roja o negra. Cada cara del cubo tiene al menos una arista negra. ¿Cuál es la menor cantidad de aristas negras que puede haber?
Solución: 3
Problema Nº 17
En la figura, XY es el arco de un círculo centrado en Z, YZ es el arco de un círculo centrado en X, XZ es el arco de un círculo centrado en Y. Si el segmento recto XY mide 1, ¿cuál es el área de la figura?
Solución:
En la figura, XY es el arco de un círculo centrado en Z, YZ es el arco de un círculo centrado en X, XZ es el arco de un círculo centrado en Y. Si el segmento recto XY mide 1, ¿cuál es el área de la figura?
Solución:
Área
= 3A+B
A
= Pedazo de torta – B
Área
= 3(pedazo de torta –B)+B
Área = 3Pedazo de torta-2B
Área del pedazo de torta (PI)*r2/6
B= área del triángulo = r*(r*SQRT(3)/2)/2 =r2*SQRT(3)/4
Área = 3(PI)*r2/6-2* r2*SQRT(3)/4
Área = r2*[(PI)/2-SQRT(3)/2]
= PI/2 – SQRT(3)/2
Área = 3Pedazo de torta-2B
Área del pedazo de torta (PI)*r2/6
B= área del triángulo = r*(r*SQRT(3)/2)/2 =r2*SQRT(3)/4
Área = 3(PI)*r2/6-2* r2*SQRT(3)/4
Área = r2*[(PI)/2-SQRT(3)/2]
= PI/2 – SQRT(3)/2
Problema Nº 18
Un entero es tartamudo si todas sus cifras son iguales a 1.
¿Cuántos enteros positivos menores que 10,000,000 cumplen que al multiplicarlos por 33 se obtiene un entero tartamudo?
Solución
Los posibles números son:
111
1111
11111
111111
1111111
11111111
111111111
Cada uno de ellos se divide entre 33
111/33 =3.36
1111/33=33.66
11111/33=336.69
111111/33=3367.00
1111111/33=33670.03
11111111/33=336700.33
111111111/33=3367003.36
Entonces el entero que se multiplica por 33 para obtener un numero tartamudo es 3367
Algunas condiciones de interés
Como se va a obtener el tartamudo multiplicado por 33, aquel debe ser múltiplo de 3 y múltiplo de 11
Solamente 111, 111111 & 111111111 son múltiplos de 3 (ya que la suma de sus cifras es múltiplo de 3)
Y para que un tartamudo sea múltiplo de 11 se requiere que tenga número par de cifras, por tanto es el 111111
Problema Nº 19
Un caminante realiza el siguiente experimento: en el primer minuto camina a 1 km/h, en el segundo minuto camina a 2 km/h, en el tercero a 3 km/h y así sucesivamente. ¿A qué velocidad estará caminando cuando haya recorrido 1000 metros?
Un caminante realiza el siguiente experimento: en el primer minuto camina a 1 km/h, en el segundo minuto camina a 2 km/h, en el tercero a 3 km/h y así sucesivamente. ¿A qué velocidad estará caminando cuando haya recorrido 1000 metros?
Solución:
Minuto Velocidad Espacio recorrido acumulado
1 1/60 1/60 1/60
2 2/60 2/60 (1+2)/60
3 3/60 3/60 (1+2+3)/60
.
.
.
n n/60 n/60 (1+2+3+...+n)/60
La velocidad será n/60 para el valor entero de n que (1+2+3+..+n)/60 = 1 k recorrido entonces.
Como 1+2+3+..+n = n(n+1)/2=60 ==> n(n+1)=120 ==> n toma valores entre [10,11], y con n = 11 se garantiza el recorrido de 1000 m o 1 kilómetro
Velocidad es 11km/hora
Problema Nº 20
¿Cuál es el valor de b − a en la siguiente figura?
Sea h la altura
h2=(x+1)2-b2
h2=(x-1)2-a2
Restando miembro a miembro
(x+1)2-b2 - (x-1)2+a2 =0
(a2 -b2) = (x-1)2-
(x+1)2
(a2 -b2) = -4x
(a-b)(a+b)=-4x
a-b=
-4x/(a+b) (recuerde a+b=x)
b-a=4x/x
b-a=4
Problema Nº 21
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los cinco puntos dados?
Solución:
ABC
ABD
ABE
ACD
ACE
ADE
BCD
BCE
BDE
CDE
En total 10 triángulos
Nota:
Es un problema de combinatoria que se resuelve de la manera soguiente:
n=5
n!=5*4*3*2*1
k=3
k!=3*2*1
Además siempre 0! = 1
Por tanto el número de triángulo es (5*4*3*2*1)/(2!*3!)=(5*4*3*2*1)/[(2*1)*(3*2*1)] = 10
Problema Nº 22
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los siete puntos dados?
ABC
ABD
ABE
ABF
ABG
ACD
ACE
ACF
ACF
ADE =7!/[(7-3)!*3!] = 35 Triángulos
ADF
ADG
AEF
AEG
AFG
BCD
BCE
BDE
.
.
.
Problema Nº 23
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los cinco puntos dados?
¿Cuántos triángulos se pueden formar uniendo cada vez tres de los cinco puntos dados?
Nota: Observe que los puntos colineales no aportan triángulos
Solución:
Número teórico de triángulos = 7!/[(7-3)!*3!] = 35 Triángulos
Pero hay cinco puntos, de la parte superior, que no aportan por ser colineales y que teóricamente aportían con 5!/(2!*3!) = 10
Y hay 3 verticales que tampoco aportan 1 triángulo.
Por tanto la solución es 35-10-1=24
Solución alterna:
Cada dos puntos de la línea horizontal se pueden unir con uno de los dos verticales finales para formar triángulos, por tanto
Es posible conseguir 5!/[(2!)*(3!)] = 10 pares diferentes, que unidos a uno de los dos puntos finales verticales da un total de 20 triángulos.
Además en la línea horizontal hay 4 puntos que pueden unirse a los dos verticales finales para formar 4 triángulos adicionales.
Todo da un total de 24 triángulos
Solución:
Número teórico de triángulos = 7!/[(7-3)!*3!] = 35 Triángulos
Pero hay cinco puntos, de la parte superior, que no aportan por ser colineales y que teóricamente aportían con 5!/(2!*3!) = 10
Y hay 3 verticales que tampoco aportan 1 triángulo.
Por tanto la solución es 35-10-1=24
Solución alterna:
Cada dos puntos de la línea horizontal se pueden unir con uno de los dos verticales finales para formar triángulos, por tanto
Es posible conseguir 5!/[(2!)*(3!)] = 10 pares diferentes, que unidos a uno de los dos puntos finales verticales da un total de 20 triángulos.
Además en la línea horizontal hay 4 puntos que pueden unirse a los dos verticales finales para formar 4 triángulos adicionales.
Todo da un total de 24 triángulos
Problema Nº 24
¿Cuántos
son los números enteros entre 100 y 400 que tienen
alguna
de sus cifras igual a 2?
Solución:
102
112
120
121
122
123
124
125
126
127
128
129
132
142
152
162
172
182
192La centena del 100 tiene 19 números.
La centena del 200 tiene 100
La centena del 300 tiene 19
Solución: 138
Problema Nº 25
Un piso cuadriculado está cubierto por azulejos cuadrados del mismo tamaño de forma que quedan alineados. Los azulejos de las dos diagonales del piso son negros. Los azulejos restantes son blancos. Si hay 101 azulejos negros, ¿cuál es el número de azulejos blancos?
Solución:
En
ambos casos la diagonal es igual al lado del cuadrado, pero el número de
azulejos de las
diagonales es impar cuando el lado del
cuadrado es impar y un un azulejo (el del
centro) es común o compartido por tanto los azulejos de las diagonales, para el caso impar, son: n+n-1 = 2n-1, ya que uno es común
Por tanto 2n-1=101 ==> n=51
y el número de azulejos blancos es igual a 51*51-101 = 2500
Problema Nº 26
Sean C1 y C2 circunferencias que se cortan en los puntos P y Q. Los radios miden 8 m y 6 m, respectivamente, y la distancia entre los centros es de 10 m. Si R es el punto de C1 diametralmente opuesto a Q, hallar la distancia de R a P.
Solución:
d = (8/10)*SQRT(100-36)
d = (4/5)*SQRT(64)
d=32/5
RP=2d=64/5=12.80
Problema Nº 27
Tengo un reloj que adelanta un minuto por día y otro que atrasa 1 1/2 minutos por día. Si los pongo simultáneamente en hora, ¿cuántos días pasarán para que ambos den simultáneamente la hora correcta?
Solución:
Problema Nº 28
Problema Nº 26
Sean C1 y C2 circunferencias que se cortan en los puntos P y Q. Los radios miden 8 m y 6 m, respectivamente, y la distancia entre los centros es de 10 m. Si R es el punto de C1 diametralmente opuesto a Q, hallar la distancia de R a P.
Solución:
El
triángulo PC1C2 es rectángulo pues sus
lados satisfacen Pitágoras
1002= 82+62
Donde
seno(C1)=6/10 =lado opuesto/hipotenusa
h=(C1P)*seno(C1)=
8*6/10=48/10
d=SQRT(82-h2)
d=SQRT(82-(48/10)2)
d=SQRT(82-(48/10)2)
d = (8/10)*SQRT(100-36)
d = (4/5)*SQRT(64)
d=32/5
RP=2d=64/5=12.80
Problema Nº 27
Tengo un reloj que adelanta un minuto por día y otro que atrasa 1 1/2 minutos por día. Si los pongo simultáneamente en hora, ¿cuántos días pasarán para que ambos den simultáneamente la hora correcta?
Solución:
Para
que, el reloj, dé un giro completo de 12 horas se requieren 12horas* sesenta minutos =720.
Como el primer reloj se adelanta un minuto, se requerírán 720días, mientras que para que el segundo reloj haga el giro completo se requieren 720/1.5 = 480.
El mínimo común múltiplo de (720,480) es 1044.
Como el primer reloj se adelanta un minuto, se requerírán 720días, mientras que para que el segundo reloj haga el giro completo se requieren 720/1.5 = 480.
El mínimo común múltiplo de (720,480) es 1044.
Problema Nº 28
Carlos, según la receta de su médico, debe tomar todo el contenido de un frasco de píldoras en 4 días de la siguiente manera: el primer día, la mitad del total; el segundo un tercio de lo que queda; el tercero, un cuarto de
lo que queda y el cuarto 6 píldoras. ¿Cuántas píldoras había originalmente
en el frasco?
Solución:
Sea x el total de píldoras
Primer día: (1/2)x
Segundo día: (1/3)(1/2)x = (1/6)x
Tercer día: (1/4)(x-x/2-(1/6)x) = (1/4)(x/2 - x/6) = (1/4)(4x/12)=(x/12)
Cuarto día: x-x/2 -x/6 - x/12 = 6
(12x-6x-2x)=6 ==> x=24
Problema Nº 29
En una mesa hay cinco cartas: Cada carta tiene de un lado un número natural y del otro una letra. Carlos afirma: Cualquier carta que tenga de un lado una vocal tiene un número par del otro lado. María demostró que Juan
Problema Nº 30
Problema Nº 31
Los boletos para entrar a la fiesta cuestan $8 para las muchachas y $10 para los muchachos. Si el precio de los boletos fuera al revés, la suma de lo que pagaron todos los que entraron a la disco sería $6 menos de lo que en realidad fue. Si asistieron 30 muchachas, ¿cuántos muchachos asistieron?
Problema Nº 32
(Olimpíada del maestro Mate)
En una ensambladora trabajan hombres y mujeres. Los hombres en varios módulos de ensamblaje con 53 operarios obligatorios cada uno, mientras que las mujeres, operan, en una única línea de embalaje, empaquetando los productos ensamblados. Como en el mes anterior no faltó ningún trabajador, el capataz decidió otorgar un bono a los trabajadores, repartidos de la manera siguiente: $4.83 para los hombres y $3.22 para las mujeres, para cuyo efecto mandó a sacar de caja, la cantidad de $8325.31 para que sean repartidos entre los trabajadores. En la repartición no sobró dinero, como era de esperarse.
Nota: La empresa trabaja, estimulando la paridad de género, por lo que la relación valor absoluto |hombres-mujeres| > 68, no está permitida.
Sean h & m la cantidad de hombres y mujeres
respectivamente.
Condiciones:
Dinero total repartido = 8325.31
Deben haber módulos completos de ensamblaje, lo que implica que los hombres pueden ser 53, 106, 159,… en general múltiplos de 53
m debe ser natural (no puede ser fracción, pues se trata de personas)
h debe ser natural (no puede ser fracción, pues se trata de personas)
El valor absoluto |Hombres – mujeres| debe ser menor o igual a 68
4.83*h+3.22*m=8325.31 (1)
Problema Nº 33
(Olimpíada del maestro Mate)
Se eliminaron dos números consecutivos de una lista de 102 números consecutivos. La suma de los que quedaron es 5232. ¿Cuáles fueron los menores números eliminados?
Solución:
(n+0) + (n+1) +(n+2) + (n+3)+… +(n+k)+(n+k+1)+…+(n+101) =
Problema Nº 37
(Olimpíada del maestro Mate)
Problema Nº 38
¿De cuántas maneras se puede escoger en un tablero de ajedrez una casilla blanca y una negra, de tal manera que no esté en las dos en una misma fila ni en una misma columna?
Solución:
Total blancas en el tablero = 32
Total negras disponibles (fuera de las columnas y filas de la blanca escogida) =24
Total de posibilidades = 32*24 = 768
Problema Nº 39
Problema Nº 40
¿Cuál es la diferencia entre el mayor y el menor divisor primo de
2^16 − 1?
Solución
a^2-b^2=(a-b)*(a+b)
2^16 − 1=(2^8-1)*(2^8+1)
=(2^4-1)*(2^4+1)*257
=(2^2-1)*(2^2+1)*17*257
=(2-1)*(2+1)*5*17*257
=1*3*5*17*257
=
El mayor primo = 257
El menir primo = 3
Diferencia= 254
Problema Nº 41
En un salón de clases hay 60 niños alineados en 6 filas y 10 columnas. Cada niño le da la mano a todos los niños que se sientan a su alrededor (incluyendo los que se sientan diagonalmente a su lado). ¿Cuántos saludos hubo?
Solución:
Problema Nº 42
Calcular el área de la región sombreada del siguiente hexágono regular, donde los círculos tienen radio 1, son tangentes entre sí y son tangentes a los lados del hexágono.
Solución:
Cálculo del lado t del hexágono
Problema Nº 43
Resolver
Solución:
Sea l el largo de la escalera, entonces
(l-10)^2 = h^2 + 5^2 (1)
Problema Nº 45
Cuál es el valor de (100-99+98-97...-1)/50
Problema Nº 46
Si se arma el siguiente troquelado, ¿cuál es el cubo que se forma?
Problema Nº 48
En la tienda de la esquina los chocolates cuestan el doble de lo que los caramelos. Comprar tres chocolates y dos caramelos cuesta 16 pesos. ¿Cuánto cuesta comprar dos chocolates y tres caramelos?
Solución:
Problema Nº 49
Paso 1: Cálculo del área del cuarto de cilindro con centro en A = PI*r^2/4 =
PI*(a/2)^2/4= PI*a^2/16
Paso 2: Cálculo del área sombreada dentro del cuadrado = a^2-3[PI*a^2/16]
Paso 3: Cálculo del área externa al cuadrado = (3/4)*PI*(a/2)^2 =3*PI*a^2/16
Paso 4: Cálculo área total = a^2 - 3[PI*a^2/16] + 3*PI*a^2/16 = a^2
Equivalente:
El área del cuadrado es a^2
Problema Nº 50
En una fiesta el 50% de los asistentes son mujeres. De las mujeres que asistieron el 30% tiene los ojos claros. Del total de asistentes a la fiesta, ¿qué porcentaje son mujeres que no tienen los ojos claros?
Solución
Sea a el total de asistentes a la fiesta, entonces
Total mujeres = a/2
Total con ojos claros = (a/2)*.3
Total sin ojos claros = a/2 - (a/2)*.3 = (a -.3a)/2 =0.7(a/2)
Porcentaje = 0.7*(a/2)/a = 0.7/2= .35 ==> 35%
Problema Nº 51
Yo rompí un papel en 10 pedazos. Mi hermanito tomó algunos de ellos y los rompió a su vez en 10 pedazos –cada uno–. Si al final quedaron 46 pedazos, ¿cuántos pedazos rompió mi hermanito?
Solución:
Sea m, h los papeles que en total suman 10 (m=míos, h=de mi hermanito)
Problema Nº 52
Carlos trabaja 4 días de la semana y descansa el quinto. En una ocasión empezó a trabajar un lunes y descansó un día domingo. ¿Cuál es la menor cantidad de días que tuvo que trabajar para que esto fuera posible?
Solución:
Problema Nº 53
En la figura, cada triángulo pequeño tiene área 1. ¿Cuál es el área de la región encerrada por las líneas negras?
Área total = 5a^2*sqrt(3)+.625*a^2*sqrt(3)=5.625*a^2*sqrt(3) = 5.625*(4/sqrt(3))*sqrt(3)=22.5
Solución:
¿Se cumple a?
Los números impares, positivos y diferentes más pequeños son: 1,3,5,7 y la suma es 16, por tanto (a) no se cumple.
¿Se cumple c?
La suma de los cuatro números es 19
Primer número = 2n-1
Segundo = 2m-1
Tercer = 2o-1
Cuarto = 2p-1
La suma de ellos es =2(n+m+o+p)-4 ==> que es par y por tanto no puede ser 19 que es impar.
¿Se cumple d?
Cada uno de los productos de dos números en diagonal es 21
21=3*7 únicamente. No hay más números menores a 20 cuyo producto sea 21
Se requieren por lo menos 4 números, por tanto (d) no cumple.
¿Se cumple b?
Sí es posible que (e) se cumpla
Problema Nº 55
Un grupo de estudiantes quiere pedir una pizza. Si cada uno de ellos coopera con $14 harían falta $4 para pagar la cuenta. Si cada uno de ellos coopera con $16, sobrarían $6 más de los que se necesitan. ¿Con cuánto debe cooperar cada uno para pagar la cuenta exacta?
Solución:
Sean n, p el número de estudiantes y el precio de la pizza respectivamente.
Entonces
n14=p - 4
n16=p+6
Restando
2n=10==>n=5
precio=14n+4=74
cada estudiante debe colaborar con 74/5 = 14.8
Problema Nº 56
En la figura ABCD y DBEF son rectángulos. ¿Cuál es el área de DBEF?
Solución:
Cáculo del segmento DB = sqrt(4^2+3^2)=5
Problema Nº 57
El reloj de mi padre se atrasa un minuto cada hora, mientras que el de mi madre se adelanta un minuto cada dos horas. Al salir de casa puse ambos relojes a la misma hora y les dije que volvería cuando la diferencia entre sus relojes fuera exactamente una hora. ¿Cuánto tiempo estaré fuera de casa?
Solución:
Relojes
Problema Nº 58
Mi edad es un número de dos dígitos que, al invertirlos, producen un número mayor al triple de mi edad. ¿Cuántas posibilidades para mi edad existen?
Solución
Si edad es de 64 años, entonces puedo escribirla como 6*10 + 4
Problema Nº 61
¿Cuántos conjuntos de enteros positivos consecutivos (dos o más) cumplen que la suma de sus elementos es igual a 100?
Solución:
n +(n+1)+(n+2)+...+(n+a)=100
n +(n+1)+(n+2)+...+(n+a)
Primer conjunto {18,19, 20, 21, 22}
Segundo conjunto {9, 10, 11, 12, 13, 14, 15, 16}
Más ejercicios en la parte II
lo que queda y el cuarto 6 píldoras. ¿Cuántas píldoras había originalmente
en el frasco?
Solución:
Sea x el total de píldoras
Primer día: (1/2)x
Segundo día: (1/3)(1/2)x = (1/6)x
Tercer día: (1/4)(x-x/2-(1/6)x) = (1/4)(x/2 - x/6) = (1/4)(4x/12)=(x/12)
Cuarto día: x-x/2 -x/6 - x/12 = 6
(12x-6x-2x)=6 ==> x=24
Problema Nº 29
En una mesa hay cinco cartas: Cada carta tiene de un lado un número natural y del otro una letra. Carlos afirma: Cualquier carta que tenga de un lado una vocal tiene un número par del otro lado. María demostró que Juan
mentía
dando vuelta sólo a una carta. ¿De cuál de las cinco cartas se trata?
Solución:
La única carta que puede ayudar es la 5 ya que si Carlos mo miente debe haber una vocal, en otro caso mentiría.
Carlos pensó tres números. Si los suma de dos en dos obtiene 38, 44 y 52, ¿cuál es el mayor de los tres números?
Solución:
Sean x,y,z los números, entonces,
x+y=38
x+z=44 ==> z-y=6
y+z=52==>2z=58 ==> z=29
x=15
y=23
Los boletos para entrar a la fiesta cuestan $8 para las muchachas y $10 para los muchachos. Si el precio de los boletos fuera al revés, la suma de lo que pagaron todos los que entraron a la disco sería $6 menos de lo que en realidad fue. Si asistieron 30 muchachas, ¿cuántos muchachos asistieron?
Solución:
Sea h el número de hombres que asistieron y x el total pagado
30*8+h*10=x
30*10+h*8=x-6
30*10+h*8=(30*8+h*10)-6
300+8h=240+10h-6
66=2h
h=33
Problema Nº 32
(Olimpíada del maestro Mate)
En una ensambladora trabajan hombres y mujeres. Los hombres en varios módulos de ensamblaje con 53 operarios obligatorios cada uno, mientras que las mujeres, operan, en una única línea de embalaje, empaquetando los productos ensamblados. Como en el mes anterior no faltó ningún trabajador, el capataz decidió otorgar un bono a los trabajadores, repartidos de la manera siguiente: $4.83 para los hombres y $3.22 para las mujeres, para cuyo efecto mandó a sacar de caja, la cantidad de $8325.31 para que sean repartidos entre los trabajadores. En la repartición no sobró dinero, como era de esperarse.
Nota: La empresa trabaja, estimulando la paridad de género, por lo que la relación valor absoluto |hombres-mujeres| > 68, no está permitida.
¿Cuántos hombres y cuántas mujeres, trabajaron el mes
pasado?
Solución:
Dinero total repartido = 8325.31
Deben haber módulos completos de ensamblaje, lo que implica que los hombres pueden ser 53, 106, 159,… en general múltiplos de 53
m debe ser natural (no puede ser fracción, pues se trata de personas)
h debe ser natural (no puede ser fracción, pues se trata de personas)
El valor absoluto |Hombres – mujeres| debe ser menor o igual a 68
4.83*h+3.22*m=8325.31 (1)
h=n*53 (2) (donde n es entero, y garantiza que h
sea múltiplo de 53)
De (1) se obtiene
m= -4.83*h/3.22 + 8325.31/4.83
De (1) se obtiene
m= -4.83*h/3.22 + 8325.31/4.83
m=-1.5*h +8325.31/4.83
m=-1.5*h +2585.50
como h=n*53
m=-1.5*n*53+2585.50 (3)
como h=n*53
m=-1.5*n*53+2585.50 (3)
m=-79.5*n+2585.50 (4)
h-m= 53n- (-79.5*n+2585.50) ==> 132.5*n-2585.50
como |h-m|≤ 68 ==>
-68≤132.5*n-2585.50≤ 68
h-m= 53n- (-79.5*n+2585.50) ==> 132.5*n-2585.50
como |h-m|≤ 68 ==>
-68≤132.5*n-2585.50≤ 68
-68 +2585.50 ≤ 132.5*n≤ 68 + 2585.50
2517.50 ≤ 132.5n ≤ 2653.50
19 ≤ n ≤ 20.026
Las soluciones están en n=19 o n=20
Las soluciones están en n=19 o n=20
Por tanto para n=19
h=n*53=1007
h=n*53=1007
m=1075
para n=20
h=1060
m=995.50 (desechada por no ser natural)
(Olimpíada del maestro Mate)
Se eliminaron dos números consecutivos de una lista de 102 números consecutivos. La suma de los que quedaron es 5232. ¿Cuáles fueron los menores números eliminados?
Solución:
(n+0) + (n+1) +(n+2) + (n+3)+… +(n+k)+(n+k+1)+…+(n+101) =
102n+ (0+1+2+3+…+k+k+1+…+101) = 102n + 5151
n + (n+1) +(n+2) + (n+3) +…+(n+k)+(n+k+1)+…+(n+101)
=
102n+5151
n + (n+1) +(n+2) + (n+3) +…+…+(n+101) +[(n+k)+(n+k+1)] = 102n+5153
5232 +[(n+k)+(n+k+1)]
= 102n+5153
5232 +(2n+2k+1) = 102n+5153
5232-5153+2n+2k+1=102n
-20+2k=100n
Se trata de lograr que -20+2k sea mútiplo de 100, y luego determinar los números borrados (n+k) & (n+k+1)
k n
10 0 ==>números borrados fueron: n+k & n+k+1 10 & 11
60 1 ==> números borrados fueron: 61 & 62
110 2
Problema Nº 34
(Olimpíada del maestro Mate)
Se dibujan un cuadrado y un triángulo ACD equilátero, ambos de lado de longitud a. Se pide hallar la longitud del segmento CB.
Problema Nº 34
(Olimpíada del maestro Mate)
Se dibujan un cuadrado y un triángulo ACD equilátero, ambos de lado de longitud a. Se pide hallar la longitud del segmento CB.
Solución:
Obtención
del punto A
Ecuación
de la recta R1 (de
pendiente -1)
y= - x+a
Distancia AC =a (dato del problema)
Coordenadas de C=(0,a)
Distancia AC =a = SQRT((0-x)2+(a-y)2))
a = SQRT(x2+(a-(-x+a))2))
a= SQRT(x2+x2)
a2 = 2x2
y= - x+a
Distancia AC =a (dato del problema)
Coordenadas de C=(0,a)
Distancia AC =a = SQRT((0-x)2+(a-y)2))
a = SQRT(x2+(a-(-x+a))2))
a= SQRT(x2+x2)
a2 = 2x2
xA=a*SQRT(1/2)
yA=a-a*SQRT(1/2)
yA=a-a*SQRT(1/2)
Punto A=(xA, yA)
Obtención del punto B
Obtención del punto B
Ecuación
de la recta R2
(y-yA)/(x-xA)=tangente(75º)
(y-yA)/(x-xA)=tangente(75º)
yB=a
(a- yA)/tangente(75º)=x-xA
xB= (a- yA)/tangente(75º)+xA
B= (xB,yB)
Obtención de la distancia CB
La distancia CB es xB
(a- yA)/tangente(75º)=x-xA
xB= (a- yA)/tangente(75º)+xA
B= (xB,yB)
Obtención de la distancia CB
La distancia CB es xB
xB= (a- yA)/tangente(75º)+xA
xA =a*SQRT(1/2)
yA =a-a*SQRT(1/2)
xB=a*SQRT(1/2)/tangente(75º)+ a*SQRT(1/2)
xB=a*SQRT(1/2)(1/tangente(75º) + 1)
Tangente(75º)=2+SQRT(3)
xB=a*SQRT(1/2)(1/(2+SQRT(3)) + 1)
xB aproximada = .8965*a
xA =a*SQRT(1/2)
yA =a-a*SQRT(1/2)
xB=a*SQRT(1/2)/tangente(75º)+ a*SQRT(1/2)
xB=a*SQRT(1/2)(1/tangente(75º) + 1)
Tangente(75º)=2+SQRT(3)
xB=a*SQRT(1/2)(1/(2+SQRT(3)) + 1)
xB aproximada = .8965*a
Problema Nº 35
(Olimpíada del maestro Mate)
Dados tres círculos: El mayor de radio r y los dos pequeño de radio r/SQRT(2), se pide la relación área B/(área total A).
(Olimpíada del maestro Mate)
Dados tres círculos: El mayor de radio r y los dos pequeño de radio r/SQRT(2), se pide la relación área B/(área total A).
Solución:
Sea B, el área común, AP área de círculo pequeño y AI área interna alos dos córculos pequeños
Problema Nº 36
(Olimpíada del maestro Mate)
Se tiene una cuadrícula de de 3xn (base 3 y altura n) cuadritos de lado 1. Si se traza una diagonal a la cuadrícula, ¿cuántos cuadritos de lado 1 son cortados por la diagonal de la cuadrícula si n=1000?
Sea B, el área común, AP área de círculo pequeño y AI área interna alos dos córculos pequeños
Área del círculo pequeño =PI(r/SQRT(2))2) = PI(r2)/2
Área del círculo grande =PI(r2) = 2*área círculo pequeño
Área
interna a los círculos pequeños
AI=AP-B+B+AP-B=2*AP-B
AI=2*AP-B
Área
externa a los círculos pequeños
AE=AG-AI=AG-(2*AP-B)=AG-2*AP+B = B
AE=B
Relación=B/B
=1
Problema Nº 36
(Olimpíada del maestro Mate)
Se tiene una cuadrícula de de 3xn (base 3 y altura n) cuadritos de lado 1. Si se traza una diagonal a la cuadrícula, ¿cuántos cuadritos de lado 1 son cortados por la diagonal de la cuadrícula si n=1000?
Solución:
Como 1000 no es múltiplo de 3, entonces la diagonal corta 1000+2 cuadritos=1002
(Olimpíada del maestro Mate)
Para alcanzar una pared de M metros de altura se construye una escalera de ladrillos de 10 cm de altura. ¿Cuántos ladrillos se requieren, como mínimo, para que la escalera alcance o sobrepase el tope de la pared?
Solución:
Caso 1
Si M es múltiplo de 10 (altura del ladrillo), entonces los ladrillos de la última columna son M/.10 = 10M
Y se trata de sumar 1 + 2 + 3 + 4 +…+ 10M = 10M(10M+1)/2 = 5M(10M+1)
Caso 2
Si M no es múltiplo de 10 (altura del ladrillo), entonces los ladrillos de la última columna son parte entera de (M/.10) +1 = P
Suponga M=2.95 y entonces M/.10 = 29.5 ( no hay 29.5 ladrillos) sino 29 +1 para que justo sobrepase a la pared
Y se trata de sumar 1 + 2 + 3 + 4 +…+ P= P(P+1)/2
Caso 1
Si M es múltiplo de 10 (altura del ladrillo), entonces los ladrillos de la última columna son M/.10 = 10M
Y se trata de sumar 1 + 2 + 3 + 4 +…+ 10M = 10M(10M+1)/2 = 5M(10M+1)
Caso 2
Si M no es múltiplo de 10 (altura del ladrillo), entonces los ladrillos de la última columna son parte entera de (M/.10) +1 = P
Suponga M=2.95 y entonces M/.10 = 29.5 ( no hay 29.5 ladrillos) sino 29 +1 para que justo sobrepase a la pared
Y se trata de sumar 1 + 2 + 3 + 4 +…+ P= P(P+1)/2
Problema Nº 38
¿De cuántas maneras se puede escoger en un tablero de ajedrez una casilla blanca y una negra, de tal manera que no esté en las dos en una misma fila ni en una misma columna?
Solución:
Total blancas en el tablero = 32
Total negras disponibles (fuera de las columnas y filas de la blanca escogida) =24
Total de posibilidades = 32*24 = 768
Problema Nº 39
Problema Nº 40
¿Cuál es la diferencia entre el mayor y el menor divisor primo de
2^16 − 1?
Solución
a^2-b^2=(a-b)*(a+b)
2^16 − 1=(2^8-1)*(2^8+1)
=(2^4-1)*(2^4+1)*257
=(2^2-1)*(2^2+1)*17*257
=(2-1)*(2+1)*5*17*257
=1*3*5*17*257
=
El mayor primo = 257
El menir primo = 3
Diferencia= 254
Problema Nº 41
En un salón de clases hay 60 niños alineados en 6 filas y 10 columnas. Cada niño le da la mano a todos los niños que se sientan a su alrededor (incluyendo los que se sientan diagonalmente a su lado). ¿Cuántos saludos hubo?
Solución:
Problema Nº 42
Calcular el área de la región sombreada del siguiente hexágono regular, donde los círculos tienen radio 1, son tangentes entre sí y son tangentes a los lados del hexágono.
Solución:
Cálculo del lado t del hexágono
t=2r/coseno(30º)
t=4r/SQRT(3)
Área hexágono
=3*SQRT(3)*t2/2
=3*SQRT(3)*16/(2*3)
=8*SQRT(3)
Área roja = 8*SQRT(3)-área de los
círculos
=8*SQRT(3)-3PI
Problema Nº 43
Resolver
Solución:
Problema Nº 44
Problema Nº 44
Contra
un muro de altura desconocida se apoya una escalera. Si el pie de la escalera está
a 5 metros del muro, el tramo de escalera que sobresale por
encima del muro mide 10 metros; en cambio, si el pie de la escalera está
a
9 metros del muro, sobresale un tramo de 8 metros de escalera. ¿Cuál
es la altura
del muro?Solución:
Sea l el largo de la escalera, entonces
(l-10)^2 = h^2 + 5^2 (1)
(l-8)^2 = h^2+9^2 (2)
Despejando h^2 e igualando
Despejando h^2 e igualando
(l-10)^2
– 25 = (l-8)^2-81
-20*l
+100 – 25 = -16*l +64 -81
4*l=75+17
4*l=75+17
4*l=92
l=23
h^2 =(l-10)^2 -25
h^2 =(l-10)^2 -25
h^2=169-25=144
h=12
h=12
Problema Nº 45
Solución 1:
(100-99) + (98-97) + (96-95) + ...+ (2-1) = 1 + 1 + 1 + 1 +...+ 1=50
(100-99+98-97...-1)/50 = 50/50 = 1
Solución 2:
100+98+96+...+2 = 2(50+49+48+...+1) = 2*50*51/2=50*51
Solución 2:
100+98+96+...+2 = 2(50+49+48+...+1) = 2*50*51/2=50*51
-99-97-95-...-1) = - (99+97+95+...+1) = - [(2*50-1) + (2*49-1)+...+(2*1-1)]
= n^2 = 50^2
(100-99+98-97...-1)/50 = (50*51-50*50)/50 = 50/50 = 1
Problema Nº 46
Respuesta: D.
Problema Nº 47
En
un triángulo ABC el ángulo en A es el
triple del ángulo en B y la mitad del ángulo en C.
¿Cuánto mide el ángulo en A?
Solución:
A + B + C = 180
A + A/3 + 2A = 180
3A + A/3 =180
10A/3=180 ==> A = 54º
Problema Nº 47
¿Cuánto mide el ángulo en A?
Solución:
A + B + C = 180
A + A/3 + 2A = 180
3A + A/3 =180
10A/3=180 ==> A = 54º
Problema Nº 48
Solución:
Sean
a & b los precios de los chocolates y caramelos, entonces:
a=2b ==>
3a +2b = 16
3(2b)+2b=16
8b=16
b=2
a=4
Luego
2a+3b=8+6=14
Problema Nº 49
Paso 1: Cálculo del área del cuarto de cilindro con centro en A = PI*r^2/4 =
PI*(a/2)^2/4= PI*a^2/16
Paso 2: Cálculo del área sombreada dentro del cuadrado = a^2-3[PI*a^2/16]
Paso 3: Cálculo del área externa al cuadrado = (3/4)*PI*(a/2)^2 =3*PI*a^2/16
Paso 4: Cálculo área total = a^2 - 3[PI*a^2/16] + 3*PI*a^2/16 = a^2
Equivalente:
El área del cuadrado es a^2
Problema Nº 50
En una fiesta el 50% de los asistentes son mujeres. De las mujeres que asistieron el 30% tiene los ojos claros. Del total de asistentes a la fiesta, ¿qué porcentaje son mujeres que no tienen los ojos claros?
Solución
Sea a el total de asistentes a la fiesta, entonces
Total mujeres = a/2
Total con ojos claros = (a/2)*.3
Total sin ojos claros = a/2 - (a/2)*.3 = (a -.3a)/2 =0.7(a/2)
Porcentaje = 0.7*(a/2)/a = 0.7/2= .35 ==> 35%
Problema Nº 51
Yo rompí un papel en 10 pedazos. Mi hermanito tomó algunos de ellos y los rompió a su vez en 10 pedazos –cada uno–. Si al final quedaron 46 pedazos, ¿cuántos pedazos rompió mi hermanito?
Solución:
Sea m, h los papeles que en total suman 10 (m=míos, h=de mi hermanito)
m+h=10==> m=10-h
10h
+ (10 –h)=46
10h
+ 10 – h =46
9h=36
h=4
Mi hermanito rompió 4 papeles
Mi hermanito rompió 4 papeles
Problema Nº 52
Carlos trabaja 4 días de la semana y descansa el quinto. En una ocasión empezó a trabajar un lunes y descansó un día domingo. ¿Cuál es la menor cantidad de días que tuvo que trabajar para que esto fuera posible?
Solución:
Tabla de descansos
1 V
2 M
3 L
4 S
5 J
6 M
7 D
8 V
9 M
Tiene que trabajar 7 turnos ==> 7*4 = 28 días
Problema Nº 53
En la figura, cada triángulo pequeño tiene área 1. ¿Cuál es el área de la región encerrada por las líneas negras?
Solución
Área total = 5a^2*sqrt(3)+.625*a^2*sqrt(3)=5.625*a^2*sqrt(3) = 5.625*(4/sqrt(3))*sqrt(3)=22.5
Problema Nº 54
En los cuadritos de la figura se escriben cuatro enteros positivos diferentes entre sí, que además son impares y menores a 20. ¿Cuál de las siguientes condiciones es posible?
(a) La suma de los cuatro números es 12.
(b) La suma de los cuatro números es 66.
(c) La suma de los cuatro números es 19.
(d) Cada uno de los productos de dos números en diagonal es 21.
(e) Cada una de las sumas de dos números en diagonal es 32.
En los cuadritos de la figura se escriben cuatro enteros positivos diferentes entre sí, que además son impares y menores a 20. ¿Cuál de las siguientes condiciones es posible?
(a) La suma de los cuatro números es 12.
(b) La suma de los cuatro números es 66.
(c) La suma de los cuatro números es 19.
(d) Cada uno de los productos de dos números en diagonal es 21.
(e) Cada una de las sumas de dos números en diagonal es 32.
Solución:
¿Se cumple a?
Los números impares, positivos y diferentes más pequeños son: 1,3,5,7 y la suma es 16, por tanto (a) no se cumple.
¿Se cumple c?
La suma de los cuatro números es 19
Primer número = 2n-1
Segundo = 2m-1
Tercer = 2o-1
Cuarto = 2p-1
La suma de ellos es =2(n+m+o+p)-4 ==> que es par y por tanto no puede ser 19 que es impar.
¿Se cumple d?
Cada uno de los productos de dos números en diagonal es 21
21=3*7 únicamente. No hay más números menores a 20 cuyo producto sea 21
Se requieren por lo menos 4 números, por tanto (d) no cumple.
¿Se cumple b?
La suma de los cuatro números es 66.
Posibles números
19
17
15
13
cuya suma es 64, por tanto (b) no se cumple.
¿Se cumple e?
Los números en diagonal suman 32
Los posibles pares son
19 & 13
17 & 15
Posibles números
19
17
15
13
cuya suma es 64, por tanto (b) no se cumple.
¿Se cumple e?
Los números en diagonal suman 32
Los posibles pares son
19 & 13
17 & 15
Sí es posible que (e) se cumpla
Problema Nº 55
Un grupo de estudiantes quiere pedir una pizza. Si cada uno de ellos coopera con $14 harían falta $4 para pagar la cuenta. Si cada uno de ellos coopera con $16, sobrarían $6 más de los que se necesitan. ¿Con cuánto debe cooperar cada uno para pagar la cuenta exacta?
Solución:
Sean n, p el número de estudiantes y el precio de la pizza respectivamente.
Entonces
n14=p - 4
n16=p+6
Restando
2n=10==>n=5
precio=14n+4=74
cada estudiante debe colaborar con 74/5 = 14.8
Problema Nº 56
En la figura ABCD y DBEF son rectángulos. ¿Cuál es el área de DBEF?
Solución:
Cáculo del segmento DB = sqrt(4^2+3^2)=5
Seno(Ø)=opuesto/hipotenusa=3/5
h= 4*Seno(Ø)=4*3/5=12/5
Área (DFEB)= base*altura=5*12/5=12Problema Nº 57
El reloj de mi padre se atrasa un minuto cada hora, mientras que el de mi madre se adelanta un minuto cada dos horas. Al salir de casa puse ambos relojes a la misma hora y les dije que volvería cuando la diferencia entre sus relojes fuera exactamente una hora. ¿Cuánto tiempo estaré fuera de casa?
Solución:
Relojes
Horas Padre Madre
1 -1 .5
2 -1*2=-2 .5*2=1
.
.
.
n -1*n=-n .5*n=.5n
Diferencia
entre un y otro = 60 minutos
.5n
– (-n)=60 = => n=60/1.5=40
Problema Nº 58
Mi edad es un número de dos dígitos que, al invertirlos, producen un número mayor al triple de mi edad. ¿Cuántas posibilidades para mi edad existen?
Solución
Si edad es de 64 años, entonces puedo escribirla como 6*10 + 4
Entonces si me edad es ab, puedo expresarla como 10a+b,
Si invierto la escritura entonces produce un número que es mayor (>) al triple de la edad
Problema Nº 59
Cada tercer día Luis dice la verdad y los demás días miente. Hoy Luis ha dicho exactamente 4 de los siguientes enunciados. ¿Cuál es el enunciado que no dijo hoy?
(a) Tengo la misma cantidad de amigas que de amigos.
(b) Soy amigo de una cantidad prima de personas.
(c) Mi nombre es Luis.
(d) Siempre digo la verdad.
(e) Soy amigo de tres personas más altas que yo.
Solución:
Caso 1: Que hoy diga la verdad
¿Es posible (a)?
Sí es posible ==> h+m=h+h=2h (h=amigos, m = amigas)
¿Es posible (b)?
No es posible, ya que el número de amigos es divisible por 2
¿Es posible (c)?
Sí es posible
¿Es posible (d)?
No es posible
¿Es posible (e)?
Sí es posible.
La conclusión es que hoy no está diciendo la verdad, y que hay dosposibles enunciados que no dijo hoy.
Caso 2: Que hoy mienta
(a) Puede ser mentira
(b) Puede ser mentira
(c) No debió ser dicha hoy
(d) Es mentira
(e) Puede ser mentira
Por tanto como hoy no miente, el enunciado que no debió decir hoy es la (c)
Problema Nº 60
En la figura se muestra un triángulo equilátero y un pentágono regular. ¿Cuánto mide el ángulo ß?
Si invierto la escritura entonces produce un número que es mayor (>) al triple de la edad
Matemáticamente
3(10a
+ b) < (10b+a)
30a +3b < 10b+a
29a < 7b
a b ¿Cumple la condición?
30a +3b < 10b+a
29a < 7b
a b ¿Cumple la condición?
1 5 si
1 6 si
1 7 si
1 8 si
1 9 si
2 9 si
3 9 no
1 6 si
1 7 si
1 8 si
1 9 si
2 9 si
3 9 no
Problema Nº 59
Cada tercer día Luis dice la verdad y los demás días miente. Hoy Luis ha dicho exactamente 4 de los siguientes enunciados. ¿Cuál es el enunciado que no dijo hoy?
(a) Tengo la misma cantidad de amigas que de amigos.
(b) Soy amigo de una cantidad prima de personas.
(c) Mi nombre es Luis.
(d) Siempre digo la verdad.
(e) Soy amigo de tres personas más altas que yo.
Solución:
Caso 1: Que hoy diga la verdad
¿Es posible (a)?
Sí es posible ==> h+m=h+h=2h (h=amigos, m = amigas)
¿Es posible (b)?
No es posible, ya que el número de amigos es divisible por 2
¿Es posible (c)?
Sí es posible
¿Es posible (d)?
No es posible
¿Es posible (e)?
Sí es posible.
La conclusión es que hoy no está diciendo la verdad, y que hay dosposibles enunciados que no dijo hoy.
Caso 2: Que hoy mienta
(a) Puede ser mentira
(b) Puede ser mentira
(c) No debió ser dicha hoy
(d) Es mentira
(e) Puede ser mentira
Por tanto como hoy no miente, el enunciado que no debió decir hoy es la (c)
Problema Nº 60
En la figura se muestra un triángulo equilátero y un pentágono regular. ¿Cuánto mide el ángulo ß?
Solución:
Cada uno de los ángulos centrales de los triángulos azules = 360/5 =72
180=2Ø+72 (por lo ángulos internos del triángulo azul)
Ø=(180-72)/2
Ø=54
Por
tanto Φ=54 (por equivalencia)
µ=180- Φ-Ø=72
ß=60+µ=132
¿Cuántos conjuntos de enteros positivos consecutivos (dos o más) cumplen que la suma de sus elementos es igual a 100?
Solución:
n +(n+1)+(n+2)+...+(n+a)=100
(a+1)n+(1+2+3+4+...a)=100
(a+1)n + a(a+1)/2=100
De la tabla se obtiene
(a+1)n + a(a+1)/2=100
De la tabla se obtiene
n +(n+1)+(n+2)+...+(n+a)
Primer conjunto {18,19, 20, 21, 22}
Segundo conjunto {9, 10, 11, 12, 13, 14, 15, 16}
Más ejercicios en la parte II


















































Estos ejercicios vienen en olimpiadas de matemáticas estatales en México, muy bien post, me sirvió
ResponderEliminarGracias. Ayude a compartir.
EliminarCual es el numero mayor de digitos posible en un producto de un numero de 2 digitos por uno por 3digitos
ResponderEliminarEl problema 27 no está resuelto correctamente, la respuesta es diferente.
ResponderEliminar