Para pasar un rato (recargado)

Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
15 abril 2014


Problema Nº 01

El lado del cuadrado mide a ¿Cuánto miden, por separado, el área azul y roja?

Solución:

Radio del círculo rojo= SQRT(2*a*a)

Área del círculo rojo = PI*(2a*a)

Área del cuadrado azul = a*a

Área del círculo amarillo = PI*a*a

Área azul = área del cuadrado azul - (1/4)área del círculo amarillo
              = a*a - PI*a*a/4

Área triángulo verde = base*altura/2 = a*a/2

Área rayada = (1/4)área del círculo amarillo - área del triángulo verde

                     = (1/4)PI*a*a - a*a/2

Área roja = (1/2)área del círculo rojo - área rayada - área azul 

                = (1/2)(2a*a*PI - [(1/4)PI*a*a - a*a/2] -[ a*a - PI*a*a/4]

                

               =  a*a*PI - (1/4)PI*a*a + a*a/2 - a*a + PI*a*a/4

               = (3/4)PI*a*a - (1/2)a*a + PI*a*a/4

               = PI*a*a - (1/2)a*a

               = a*a(PI - 1/2)


Problema Nº 02

Fati sale, del punto A, en automóvil a las 7:00 de la mañana. Carlos que va al doble de velocidad sale también del punto A, alcanza,a Fati, exactamente a la mitad del camino y llega 1.5 h antes al lugar de destino común. ¿A qué hora salió Carlos, y cuánto tardó en hacer el viaje? 

Solución:

Sea X la longitud del camino, to el tiempo de retraso de Carlos, Tf y Tc tiempo que consumen Fati y Carlos para llegar y Vf y Vc las velocidades respectivas, entonces

Espacio recorrido por Fati = (Vf)*Tf

Espacio recorrido por Carlos = (Vc)*Tc

Como Vc = 2 VF
         Tc = Tf-1.5 - to

Vf*Tf=(2Vf)*Tc

Vf*Tf=(2Vf)*(Tf-1.5-to)

Tf = 2(Tf-1.5-to)

2to+3=tf

tf = 2to + 3

tf = (to + 1.5) + (to +1.5) = MITAD + MITAD (porque a mitad de tiempo pasan por el punto medio)

Entonces Carlos tarde 3 horas y llega 1.5 horas antes y salió 1.5 horas después.

Problema Nº 03

Carlos distribuyó la misma cantidad de canicas entre cada uno de 6 compañeros y se tomó 4 para sí. Si la cantidad inicial era un número múltiplo de 7 entre 50 y 70...¿Cuántas canicas tenía y cuántas recibio cada compañero?

Solución:

Sean x, número entero, las canicas recibidas por cada compañero,

Total canicas = 6x+4

6x+4=56
x=52/6 (no es posible)


6x+4=63
x=59/6  /no es posible)

6x+4=70
x=66/6=11

Carlos tenía 70 canicas y repartió a cada jugador.


Problema Nº 04

Encontrar la relación de áreas del paralelogramo con la del rectángulo.

Solución:

Primera parte:

área del rectángulo = 3b*3a=9ab

Segunda parte:

área del triángulo superior derecho = b*2a/2=b*a

área del triángulo superior izquierdo = a*2b/2 =a*b

área del paralelogramo = área del rectángulo -(áreas de los triángulos grises)

                                 = 9ab - (4ab)=5ab

Relación:

5ab/9ab = 5/9

Problema Nº 05

Considere 48 canicas repartidas en tres montones A, B y C de manera que si del montón A pasa al B tantas canicas como hay en el B, luego del B pasa al C tantas canicas como hay en el C y del C pasa al A tantas como existen ahora en el A, tendrá el mismo número de canicas en cada montón. ¿Cuántas canicas había al principio en cada montón? 

Solución:

Sean XA1, XB1 y XC1 las cantidades iniciales
 

XA2=XA1-XB1 (se pasan al montón B)

XB2=XB1+XB1 = 2XB1 (se reciben del montón A)

XB3=2XB1-XC1 (se pasan al montón C)

XC2=XC1+XC1 =2CX1 (se reciben del montón A)

XC3=2XC1-(XA1-XB1) = 2XC1-XA1+XB1 (se pasan al montón A)

XA3=XA1-XB1+(XA1-XB1) = 2XA1-2XB1 (se reciben del montón C)

 Entonces:

 XA3=XB3 (condiciones finales)

 XB3=XC3 (condiciones finales)

AX1+BX1+CX1=48 (condiciones iniciales)

   XA1 +   XB1 +   XC1 = 48

2XA1  - 4XB1 +   XC1 =  0

  XA1 +    XB1 - 3XC1 =  0

XA1=22

XB1=14

XC1=12

Problema Nº 06

¿El resultado de la operación siguiente: 1-2-3+4+5-6-7+8+ ... -1998-1999+2000 es?  

Solución:

    1-2-3+4+5-6-7+8+9-10-11+...-1998-1999+2000

=  1-2-3+4+5-6-7+8+9-10-11+...-1998-1999+2000+2001 - 2001

=  1+4+4+4+...+4 - 2001

=  1+500*4 -2001

=  0

Problema Nº 07

¿Si el perímetro de la flor es a ¿cuál es el radio del círculo?

 Solución:


 Se trata de determinar la longitud del arco que encierra 120º

2PI*r ----->  360º
  X    ----->  120º

X=(2/3)PI*r

Como son 6 arcos el perímtero es 6*(2/3)PI*r = 4pi*r

Como el perímetro es a ==> a=4PI*r ==> r=a/(4PI)


Problema Nº 08

Carlos compró caramelos de 5 colores; 420 de eran blancos, 421 amarillos, 422 rojos, 423 verdes y 424 marrones y se los comió de la siguiente forma: Sin mirar sacaba tres de la bolsa. Si los tres eran del mismo color, se los comía, caso contrario, los regresaba a la bolsa. Continuó así hasta que sólo quedaron cuatro caramelos en la bolsa. ¿De qué color eran? 

Solución

420=420

421=420+1 Amarillo

422=420+2 Rojos

423=423

424=423+1 Marrón

Problema Nº 09

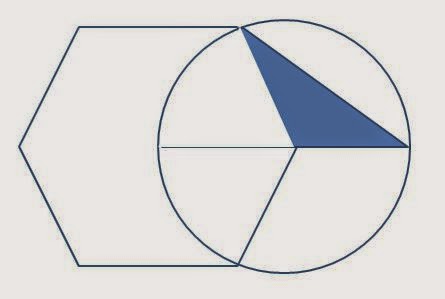
 Hallar la razón del área azul entre el área del hexágono regular.

 Solución: 

Área azul =r*h/2

Área hexágono=6*r*h/2=3rh 

Relación =(rh/2)/(3rh)=1/6

                 
Problema Nº 10

Al dividir un número x entre 2 sobra 1, entre 3 sobra 2, entre 4 sobra 3 ¿Cuánto sobra cuando se divide entre 5?

Solución:

Sean a,b,c enteros

X = a2+1
X = b3+2
X = c4+3

Entonces:

a2+1=b3+2 ==> a=(b3+1)/2
b3+2=c4+3 ==> b= (c4+1)/3

Una solución

c=2
b=3
a=5 todos son enteros

X=11 (al dividir entre 5 sobra 1)

Otra solución

c=5
b=7
a=11 todos son enteros

X=23


Problema Nº 11

Si al numerador de una fracción se añade 5, el valor de la fracción es 2, y si al numerador se resta 2 el valor de la fracción es igual a 1. Hallar la fracción.

Solución:

Sean X, Y números enteros

X/Y la fracción

(X+5)/Y = 2 ==> Y=(x+5)/2

X/(Y-2)  =1  ==> Y=X+2

Por tanto

2X+4=X+5 ==> X =1

Y=3


Problema Nº 12

Dados los dos triángulos equiláteros,  halle el ángulo ?

Solución:

Se forma el triángulo isóceles de ángulos ?, ? y (60+Φ)

?+?+((60+Φ) =180º

? = (120-Φ)/2

Problema Nº 13

Si BC = AD, ¿Cuánto vale el ángulo ADC?

Solución:

El ángulo BAC es 75º, por tanto el triángulo ABC es isóceles y AC = BC. El triángulo ACD es también isóceles y el triángulo ADC es 50º.

Problema Nº 13

Si aa = 224  &  bb = 318  hallar aa-b

Solución:

224 =(23)8 = 88  ==> a = 8

318 =(32)9 = 99  ==> b = 9

aa-b =88-9 = 8-1 = 1/8

Problema Nº 14

Determinar la figura que sigue en la secuencia:

 
Solución:

Problema Nº 15

Si el radio del círculo marrón es nR, donde R es el radio del círculo rojo, ¿Cuántas vueltas dará el círculo rojo alrededor del marrón hasta regresar al punto de partida?

Problema Nº 16

Si a cada factor de un producto de dos factores se incrementa en c unidaddes entonces ¿cuánto se incrementa el nuevo resultado?

Solución:

sea P el producto de a*b

P=(a+c)*(b+c)=ab+ac+bc+ c2=ab+c(a+b+c)

El incremento es c(a+b+c)

Problema Nº 17

Hallar la suma de las cifras del menor número de dos cifras que aumentado en 12 da un cuadrado perfecto. 

Solución:

El primer cuadrado perfecto después del 12 es 16, por tanto las cifras del menor número de dos cifras deben sumar 4.

13

31

40

22

Como piden el menor, la solución es 13.

Problema Nº 18

Para cada x∈ℛ; se define f(x) como: “el mayor entero que es menor o igual a x”. Determine el valor de: f(f(f(-2,8) + 3,5)-1)

Solución:

f(f(f(-2,8) + 3,5)-1)

f(f(   -3 + 3,5)-1)

f(f(0.5)-1)

f(0-1)

f(-1)=-1 (Recuerde se trata del mayor entero menor o igual a x.

 

Problema Nº 19

La población masculina de cierta ciudad se compone de 100 hombres,50 de ellos están actualmente casados en primeras o segundas nupcias, 33 no se casaron nunca, 20 enviudaron y 5 se separaron de su primera mujer y no volvieron a casarse. ¿Cuántos de los que enviudaron volvieron a casarse?

Solución:

50-x+x+20-x+33+5=100 

X= 8

Problema Nº 20 

Se dispone de 64 columnas de monedas, y una de ellas es falsa (todas las monedas son falsas y todas pesan n gramos más que las verdaderas) ¿Cúal es el mínimo de pesadas, deben hacerse para encontrar la columna falsa? 

Solución: 

Paso 1: Se toman 32 y 32 y se pesan y se desecha el montón que pesa menos.

Paso 2. Se toman 16 y 16 y se pesan y se desecha el montón que pesa menos.

Paso 3. Se toman 8 y 8 y se pesan y se desecha el montón que pesa menos.

Paso 4. Se toman 4 y 4 y se pesan y se desecha el montón que pesa menos.

Paso 5. Se toman 2 y 2 y se pesan y se desecha el montón que pesa menos.

Paso 6. Se toman 1 y 1 y se determina la falsa.

Total 6 pasos.

Sugerencia: Y para un millón de columnas, ¿cuántos pasos se requieren?


Problema Nº 21

Un lechero tiene un camión cisterna de leche y desea vender diez litros de leche y sólo tiene una cántara de ocho y una de tres litros. ¿Cómo hace para pasar la leche a la vasija del comprador?

Solución:

Paso 1. Pone dos cántaras de 3l. de leche en la cántara de 8

Paso 2. Llena la cántara de 8 litros y le queda 1 litro en la cántara de 3 que se lo entrega al cliente, luego le entrega al cliente 3 cántaras llenas de 3 litros  y listo.

Problema Nº 22

Se requieren cuatro litros de agua. ¿Cómo lograrlo con dos jarras sin graduar, una de 5 l. y otra de 3 l?

Solución:

Paso 1: Se llena una jarra de 5 l. y se pasa a la de 3. Quedan 2 en la de 5 l.

Paso 2. Se vacía la de 3 l. y se pasan a ella los 2 l. que quedaban en la de 5.

Paso 3. Se llena la de 5 l. y se pasa el litro faltante a la de 3. Quedan los cuatro requeridos en la de 5.

Problema Nº 23

Se encuentran dos viajeros en un tren y entablan una conversación:

- Tengo tres hijos. El producto de sus edades es 36 y la suma, el mismo número del asiento en el que estás.
- Hay dos soluciones pero ¿los mayores son los gemelos?
- No, los chicos.
- Entonces, ya se la solución.
¿Cuáles son las edades de los tres hijos?, y ¿por qué pregunta eso?

Solución

36             2
18             2
  9             3
  3             3

36 = 2*2*3*3    Sería 4 hijos
36 =2*2*9        Serían 3 hijos
36= 4*3*3        Serían 3 hijos
36=2*6*3         Serían 3 hijos

El problema en verdad tiene tres soluciones, y no dos, como plantea el ejercicio


Problema Nº 24

El director de una banda de menos de 50 músicos de un pueblo de León estaba desesperado. Hiciese como hiciese la formación de sus músicos para desfilar, siempre le sobraba uno que se llamaba Cano y tocaba los platillos. Si colocaba a los músicos de 4 en fondo, le sobraba uno, el pobre Cano que tenía que ir solo al final; si formaban en columna de a tres, el problema seguía siendo el mismo: Cano y sus platillos otra vez solos al final. Incluso cuando la banda desfilaba de dos en dos ocurría igual.
Luisa, la mujer de Cano, que era una gran observadora, propuso al director que los colocase de 5 en fondo. Este le hizo caso y, ¡sorpresa!, todas las filas quedaron completas, ya no sobraba el pobre Cano.

¿Cuántos músicos tenía la banda?

Solución:

Sea x el número de músicos

x =a4+1
x=b3+1
x=c2+1
x=d5+0

Condición sine qua non: a,b,c,d deben ser enteros

4a+1=3b+1 ==> a=(3/4)b
3b+1=2c+1 ==> b=(2/3)c

Tanteo de solución Nº 1:

c=6
b=4
a=3

==> x=13 que no satisface = 5d (no es múltiplo de 5)

Tanteo de solución Nº 2:

c=9
b=6
a=9/2 rompe la condición que a debe ser entero

==> x=13 que no satisface = 5d (no es múltiplo de 5)

Tanteo de solución Nº 3:

c=12
b=8
a=6

==> x=25 que si satisface = 5d (es múltiplo de 5)

Solución: La banda tenía 25 músicos 


Problema Nº 25 

Tengo un rollo de cuerda de menos de 100 m. Si lo mido de 2 en 2 m. me sobra 1m., si lo mido de 3 en 3 m., me sobran 2 m., si de 4 en 4 me sobran 3, si de 5 en 5, me sobran 4 y si de 6 en 6 me sobran 5.  ¿Cuánto mide el rollo? 

Solución:

x=2a+1

x=3b+2

x=4c+3

x=5d+4

x=6e+5

 ab,c,d,e son enteros

2a+1=3b+2==>a=(3b+1)/2

3b+2=4c+3==>b=(4c+1)/3

4c+3=5d+4==>c=(5d+1)/4

5d+4=6e+5==>d=(6e+1)/5

e=9

d=11

c=14

b=19

a=29

El número es 59