3: Ejercicios de aptitud numérica con respuesta

Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
23 marzo 2014


Problema Nº 1

Conseguir el siguiente término de 1; 2; 4; 8,...

Respuesta: 16

En videos:

En Youtube hacer clic aquí.

En FaceBook hacer clic aquí.

Problema Nº 2

Conseguir el siguiente término de la sucesión:

0; 3; 8; 15; ...

Respuesta: 24

En videos:

En Youtube hacer clic aquí.

En FaceBook hacer clic aquí.

Problema Nº 3

Una llave defectuosa deja pasar una gota de agua de 2 mm de diámetro cada 10 segundos. ¿En un mes cuántos litros cúbicos se desperdiciarán?

Respuesta: 1086 lt.
 
Volumen de la gota: (4/3)πR²

Radio de la gota: 1mm = (1/3) M³

Volumen de la gota = (4/3)*3,14126*1 = 0,00418879 M³

Segundos del mes = 30*24*60*60 (días*mes*horas*minutos*segundos) = 2592000

Bloque de 10 segundos = (Segundos del mes)/10 = 2592000/10 = 259200

Volumen del agua por mes =  (0,00418879 M³ )*259200 = 1086 lt. 

Problema Nº 4

Un cliente debe $200 en una tienda de electrodomésticos. Si paga enseguida le harán un descuento de 13%. ¿Cuánto debe pagar de aceptar la propuesta?

Respuesta: 174


Problema Nº5

Un comerciante compra un producto en 174, si lo vende con un margen de ganancia de 13%, ¿En cuánto debe venderlo?

Respuesta: 196.62

Nota: Explique por qué la diferencia entre los problemas 4 & 5


Problema Nº 6

3/8 de un grupo viste de rojo, 3/5 de amarillo y el resto de verde ¿Qué porcentaje viste de verde?
 
Respuesta: 2.5%


Problema Nº 7

Tengo 20 monedas de 25 centavos, 7 de 50 centavos y 120 de un centavo, cuánto dinero tengo?

Respuesta: 9.70


Problema Nº 8
 
¿El valor de 12²-4³ es igual a 5*4²?

Respuesta: Sí.


Problema Nº 9

 Una persona estudia de acuerdo a la relación:

40% de una hora el día martes
50% de una hora el miércoles
30% de una hora el viernes.

¿Cuánto estudia en minutos?

Respuesta: 72 minutos


Problema Nº 10

Tres medios de un número es igual al número aumentado en 10, entonces la mitad del número es:

Respuesta: 10


Problema Nº 11

¿Cuál es la fracción generatriz de 0.12345?

Respuesta: 12345/100000


Problema Nº 12

Hallar cuatro números cuya suma sea 18. El segundo es la mitad del primero, el tercero es la mitad del segundo y el cuarto es el doble del tercero. 

Respuesta:

X=8

Y=4

Z=2

W=4

Problema Nº 13

La semisuma de dos números es 12 y su semidiferencia es 4 ¿cuál es el mínimo común múltiplo de dichos números?

Respuesta:16


Problema Nº 14

El área de un círculo es A mientras que la de otro círculo es A/2. ¿Cuál es la relación entre los radios?

Respuesta: El radio del círculo pequeño es R/SQRT(2) ==> r = R/√2

Nota: Recuerde que SQRT significa raíz cuadrada 


Problema Nº 15

Cuál es el número que sumado a una tercera parte da como resultado 81.

Respuesta: 243/4


Problema Nº 16

En un café la razón entre hombres y mujeres es de 200 a 300. Si una mujer abandona el café la razón pasa a ser 1. ¿Cuántos hombres y mujeres habían inicialmente en el café?

Hombres=2
Mujeres=3


Problema Nº 17

Los catetos de un triángulo miden 3 y 4m respectivamente, ¿cuánto mide el lado faltante?

Respuesta: 5


Problema Nº 18

El promedio de gastos semanales de una personas es de $32. El domingo gasta $10, ¿cuál es el promedio de gastos diario de lunes a sábado?

Respuesta:3,67


Problema Nº 19

Un cliente paga $15503.40 por un vehículo cuyo precio oficial de venta es $16200, ¿de cuánto fue el descuento?

Respuesta: 4,3%


Problema Nº 20

Juan compra un carro en 15500 y lo va a vender ganando un 4.3%, ¿en cuánto debe venderlo?

Respuesta: 16166.50


Problema Nº 21

Carlos vende un producto en 1380, si su margen de ganancia fue de 15%, ¿en cuánto lo compró, y cuánto ganó?

Respuesta: 1200


Ganancia: 180

 
Problema Nº 22

Carlos vende un producto en 1380. En el precio de venta está incluída una ganancia de 180, ¿cuál fue el margen de ganancia sobre la venta?

Respuesta: 13.043% 


Problema Nº 23

62+4-2 es igual a:

Respuesta: 577/16


Problema Nº 24

Si Carlos puede recorrer en bicicleta 50 metros, mientras Ana camina 25 ¿Cuántos metros recorre Carlos mientras Ana camina 30 

Respuesta: 60

  

Problema Nº 25

El valor de 1/10 + 1/100 + 1/1000 es?

Respuesta: 111/1000

  

Problema Nº 26

Hallar el ángulo x

Respuesta 95º

Problema Nº 27

¿El ángulo barrido por el horario de un reloj durante los 75 minutos es?

Respuesta: 37.5º

Problema Nº 28

Un frasco que contiene cien monedas iguales pesa 1400g. Si el frasco vacío pesa 200g entonces el peso, en gramos, de una moneda es:

Respuesta: 12

Problema Nº 29

El volumen de un cubo es 216 cm³. El área, en centímetros cuadrados, de la superficie del cubo es

Respuesta: 216


Problema Nº 30

El radio de cada uno de los semicírculos pequeños es R. Hallar el perímetro de la figura.

Respuesta:

6*PI*R 

Problema Nº 31

A, B, C escogieron, cada uno, un regalo de cumpleaños para su mamá. Luego decidieron combinar los tres precios y pagar cada uno el mismo monto. Si cada uno de ellos hubiera pagado el valor del regalo que escogió, A habría pagado $1000 más, B $3000 menos y C habría pagado $20000. El total de los precios de los tres regalos fue:

Respuesta: 54000

Problema Nº 32

Cuando se expresa 10⁹⁷ - 97 como un número en representación decimal común, ¿cuál es la suma de sus dígitos?

Respuesta: 858


Problema Nº 33

A 1 km del centro del pueblo hay un aviso que reza 120 km/h, a 1/2 km del centro un aviso dice 60 km/h, a 1/3 km hay un aviso que reza 40 km/h, a una distancia de 1/4 km el aviso dice 30 km/h, a 1/5 un aviso reza 24 km/h y a una distancia de 1/6 el aviso dice 20 km/h. Se pregunta: ¿Cuánto tiempo tarda en llegar al pueblo, luego de que el conductor vio el primer aviso?

Respuesta: 73.5 segundos.


Problema Nº 34 

¿Cuántos ejes de simetría hay, sin tomar en cuenta los colores?

Respuesta: 2



Problema Nº 35 

¿Qué croquis puede ser doblado para formar el cubo que se muestra?

 Solución:

Problema Nº 36 

¿La mayor cantidad de días lunes que pueden darse en un período de 50 días consecutivos es:

Respuesta: 8


Problema Nº 37 

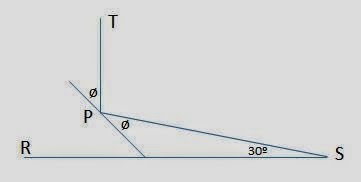
Un rayo de luz es emitido por una fuente puntual S, se refleja en un espejo en el punto P, y llega a un punto T tal que PT es perpendicular a RS. Entonces Ø es:

 Solución:

Problema Nº 37 

En el triángulo rectángulo, el arco con centro en P y radio PR corta a PQ en S. La razón entre el área de PRS y el área de RSQ es:

Respuesta: PI/(4-PI)

Problema Nº 38 

Si se puede sentar un pasajero adelante y tres pasajeros atrás en un cierto taxi, ¿de cuántas maneras diferentes se pueden acomodar cuatro pasajeros en el taxi si uno de los pasajeros se niega a sentarse adelante? 

Problema Nº 39

¿Cuántos años del siglo XXI tendrán la propiedad de que, si se divide el número del año por cada uno de los números 2, 3, 5 y 7 siempre se obtiene residuo 1? 

Respuesta: 0

Problema Nº 40

El área del cuadrado es 1 unidadad de área, ¿cuánto vale el área del paralelogramo?

Respuesta: 1/8

Problema Nº 41

El semicírculo PRQ con diámetro PQ tiene centro en O. M es el punto medio de OQ y RM PQ. El valor de la razón PR:RM es:

Respuesta: 2


Problema Nº 42

En un grupo de 40 estudiantes, 20 juegan tenis, 19 juegan voleibol y 6 juegan tanto tenis como voleibol. El número de estudiantes del grupo que no juegan ni tenis ni voleibol es:

Respuesta: 7

Problema Nº 43 

Hay 16 equipos en la primera división de fútbol de un cierto país. Los equipos pertenecen a dos divisiones de 8 equipos cada una. Cada equipo juega un partido con cada uno de los otros equipos en su propia división, luego un partido con cada uno de los equipos de la otra división y completa la temporada jugando nuevamente un partido con cada uno de los demás equipos de su propia división. ¿Cuántos partidos se juegan en total en una temporada? 

Respuesta: 176

Problema Nº 44 

Si 2^x = 10 entonces 32^x es igual a

Respuesta= 100.000

Problema Nº 45 

La cantidad de mililitros de agua que debe añadirse a 350 mL de refresco de naranja que contiene un 50 % de jugo para hacer un refresco que contenga un 30 % de jugo es:

Respuesta: 3675/9

Problema Nº 46

Si a es mayor que b en un 50% y b es mayor que c en un 25%, entonces ¿En qué porcentaje es a mayor que c?

Respuesta: 87.50%

a = b*1.5

b = c*1,25

Entonces

a = (c*1,25)*1,50

a = c*1,875

Problema Nº 47 

En 1977 Ricardo tenía 20 años y sus hermanos 6 y 7 años respectivamente 

¿cuál es el menor número de años que debe transcurrir a partir de ese año

para que la edad de Ricardo llegue a ser menor o igual que la suma de las edades que tendrán sus dos hermanos?

Respuesta: x=7