
Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
07 junio 2014
Problemas para ayudarlo en su graduación de mate
Problema Nº 1
Se tienen tres recipientes que contienen cada uno cierta cantidad de agua. Si se vierte 1/2 del agua del primero en el segundo y luego 1/3 del agua del segundo en el tercero y por último, se extrae 5 lt del tercero que se vierten en el primero, quedando cada uno con 10 lt ¿Qué cantidad de agua tenía cada vasija?
Solución:
Primer recipiente: P ==> P-P/2+5 = cantidad final = 10
Segundo recipiente: S ==>S+P/2-(1/3)(S+P/2) = cantidad final = 10
Tercer recipiente: T ==>T + (1/3)(S+P/2)-5 = cantidad final = 10
Primer: P-P/2+5=10 ==> P =10
Segundo: S+P/2-(1/3)(S+P/2)=10
Primer recipiente: P ==> P-P/2+5 = cantidad final = 10
Segundo recipiente: S ==>S+P/2-(1/3)(S+P/2) = cantidad final = 10
Tercer recipiente: T ==>T + (1/3)(S+P/2)-5 = cantidad final = 10
Primer: P-P/2+5=10 ==> P =10
Segundo: S+P/2-(1/3)(S+P/2)=10
(2/3)S
+P/2 -P/6 =10
(2S/3)=10-P/3
2S/3=(30-10)/3
2S=20
S=10
Tercero: T+(1/3)(10+5)-5=10
Tercero: T+(1/3)(10+5)-5=10
T=10
Problema Nº 2
En una sala rectangular que tiene 4 metros más de largo que de ancho, se coloca una alfombra rectangular que deja al descubierto un margen de 1 metro por cada lado. El total de la superficie descubierta es igual a la mitad de la superficie de la alfombra. ¿Cuál es el área de la alfombra y cuál el perímetro de la sala?
Problema Nº 2
En una sala rectangular que tiene 4 metros más de largo que de ancho, se coloca una alfombra rectangular que deja al descubierto un margen de 1 metro por cada lado. El total de la superficie descubierta es igual a la mitad de la superficie de la alfombra. ¿Cuál es el área de la alfombra y cuál el perímetro de la sala?
Solución:
Área descubierta = 2*[(a+4) + (a-2)] = 2(a+4+a-2)=2(2a+2)=4a+4
Área descubierta = 2*[(a+4) + (a-2)] = 2(a+4+a-2)=2(2a+2)=4a+4
Área alfombra = (a+4-2)*(a-2)=(a-2)(a-2)=a^2-4
Por relación de áreas ==> (1/2)*(a^2-4) = 4a+4 ==> a^2-4=8a+8
a^2 -8a - 12 ==> a=(8+sqrt(64+48))/2=4+2*sqrt(7)
Área descubierta = 4a+4=16+8*sqrt(7)+4=20+8sqrt(7)
Área roja= (4+2sqrt(7))^2 - 4 = 16+16sqrt(7)+28 -4 = 40 +16sqrt(7) =2*área descubierta.
Perímetro de la sala= 2(a+4+a) = 4a+8 =4(4+2*sqrt(7))+8 = 8sqrt(7)+24.
Problema Nº 3
En un zoológico habitan juntos dromedarios, avestruces y camellos. Si habían 12 cabezas, 11 gibas y 40 patas, ¿Cuántos animales hay de cada tipo?
Solución:
Sean d,a y c los animales entonces:
d+a+c=12 (cabezas)
2d+c=11 (gibas)
4d+2a+4c=40 (patas)
Resolviendo
d=3
a=4
c=5
Problema Nº 4
Problema Nº5
De acuerdo a la siguiente secuencia 0, 2, 6 12, 20,... ¿Cuál es el número de la posición 10?
Solución:
Problema Nº 6
Cierta bacteria, luego de una hora de ser introducida en un estanque, engendra otra bacteria y así cada hora mientras esté viva. Cada bacteria luego de una hora de engendrada, comienza el mismo ciclo de reproducción de la "bacteria madre".
De esta manera si ninguna bacteria ha muerto, ¿Cuántas bacterias habrá luego de 13 horas de haberse introducido la primera bacteria al estanque?
Solución:
En la hora 0 hay una bacteria,
En la hora 1, está la primera y una que engendra (roja)
En la hora 2, la verde + la roja que engendra, y la roja se vuelve verde y engendra una roja y así sucesivamente.
En la hora 13 hay 2^13 bacterias.
Problema Nº 7
El área del triángulo isósceles es 8 cm^2, y AC es un semicírculo, entonces ¿cuánto mide el área roja?
Solución:
Área del triángulo = r*r/2=8==> r=4
Pedacito de torta blanca por debajo de la recta AC= Pedazo completo - área del triángulo isósceles = PI*r*r/4-8= PI*16/4-8 =4*(PI-2)
Pedacito de torta blanca por debajo de la recta AC= Pedazo completo - área del triángulo isósceles = PI*r*r/4-8= PI*16/4-8 =4*(PI-2)
Área
roja = área semicírculo rojo – área del pedacito de torta blanca
= PI*(l/2)^2/2-4(PI-2)
= PI*(2r*r/4)/2-4(PI-2)
= PI*4 - 4PI+8
= 8
Problema Nº 8
La suma de los 6 primeros términos de una progresión geométrica es igual a 9 veces la suma de los 3 primeros términos. EL valor de la razón es?
Solución:
a+ar+ar^2+ar^3+ar^4+ar^5=9(a+ar+ar^2)
a(1-r^6)/(1-r)=9a(1-r^3)
(1-r^3)(1+r^3)=9(1-r^3)
1+r^3=9
r^3=8
r=2
Problema Nº 9
De 7 estudiantes de ingeniería y 4 de administración se va a formar un comité de 6 estudiantes para cierta investigación. ¿De cuántas maneras se puede formar este comité, si tiene que haber al menos 2 estudiantes de administración?
Solución:
Problema Nº 10
Una mesa cuadrada tiene una silla a cada lado, de las cuales dos las ocupan mujeres y una la ocupa un hombre, entonces se puede afirmar, con certeza que:
A. Las mujeres están a la par.
B. Las mujeres están de frente.
C. El hombre esta frente a una mujer.
D. El hombre está junto a la silla vacía.
E. Una mujer está junto a la silla vacía.
Respuesta E.
Problema Nº 11
Luis y Natalia, compitieron en un torneo de natación. La distancia recorrida por Luis, con 2 brazadas fue la misma que recorrió Natalia con tres brazadas. Además Luis duró 1.5 s dando cada brazada, mientras que Natalia duró 1 s por brazada.
¿Quién ganó la competencia?
Solución:
Luis 2 brazadas para recorrer d
Natalia
3 brazadas para recorrer d
Luis 1.5 brazadas/segundo
Luis 1.5 brazadas/segundo
Natalia
1 brazada/segundo
Distancia total L
Cuántos tramos d = L/d
Brazadas=
Brazadas=
Natalia
= (L/d)*3
Luis
= (L/d)*2
Tiempo de natalia= (L/d)*3
Tiempo
de Luis = (L/d)*2*1.5= (L/d)*3
Empataron
Empataron
Problema Nº 12
Cada uno de los tres números mostrados representa el perímetro del rectángulo que lo contiene. El perímetro del rectángulo marcado con la X es:
Solución:
2(a+b)=2 ==>
2a + 2b = 2 (1)
2(c+a)=1 ==> 2c + 2a = 1 (2)
2(d+b)=x ==> 2d + 2b = x (3)
2(d+c)=2 ==>
2d + 2c = 2 (4)
Sumando 1 & 4
2a+2b+2d+2c=4
2a+2b+2d+2c=4
2a + x + 2c = 4
2c + 2a + x =4
1 + x =4 ==> x=3
Problema Nº 12
En una fábrica embotelladora, se tienen 3 máquinas (A, B y C). Por cada 7 botellas que produce la máquina A, la máquina B produce 5 y, por cada 3 botellas que produce la máquina B, la máquina C produce 2. En un día, la máquina A produjo 4400 botellas más que C. ¿Cuántas botellas produjo la máquina B ese día?
Solución
Producción
A=A
B=(5/7)A
C=(2/3)B=(2/3)(5/7)A=(10/21)A
A-C=4400 ==> A-(10/21)A=4400 ==>(11/21)A=4400 ==> A = 21*400=8400
B=(5/7)8400==>B=5*1200=6000
Problema Nº 13
Maestro Mate
¿Puedes explicarme, pero matemáticamente, como funcionan las pirámides financieras?
Claro, pequeño capitán, y el algoritmo lo usaré para multiplicar el conocimiento conectivo.
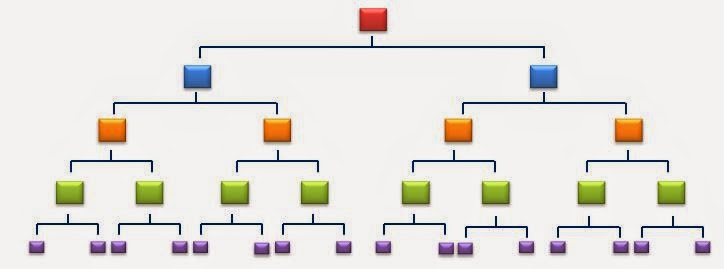
Te dejo el gráfico con el cual desarrollaré la teoría que luego publicaré como ejercicio en mi blog
2a+2b+2d+2c=4
2a + x + 2c = 4
2c + 2a + x =4
1 + x =4 ==> x=3
Problema Nº 12
En una fábrica embotelladora, se tienen 3 máquinas (A, B y C). Por cada 7 botellas que produce la máquina A, la máquina B produce 5 y, por cada 3 botellas que produce la máquina B, la máquina C produce 2. En un día, la máquina A produjo 4400 botellas más que C. ¿Cuántas botellas produjo la máquina B ese día?
Solución
Producción
A=A
B=(5/7)A
C=(2/3)B=(2/3)(5/7)A=(10/21)A
A-C=4400 ==> A-(10/21)A=4400 ==>(11/21)A=4400 ==> A = 21*400=8400
B=(5/7)8400==>B=5*1200=6000
Problema Nº 13
Maestro Mate
¿Puedes explicarme, pero matemáticamente, como funcionan las pirámides financieras?
Claro, pequeño capitán, y el algoritmo lo usaré para multiplicar el conocimiento conectivo.
Te dejo el gráfico con el cual desarrollaré la teoría que luego publicaré como ejercicio en mi blog
Solución:
Mientras más arriba más vivo, mientras más abajo menos vivo.
El
señor rojo decide montar una pirámide de
estructura 2 (cantidad de subordinados), va a cobrar una cantidad n de dólares por la inscripción a cada uno de sus primeros
dos subordinados que
pertenecen al estrato azul (no tan vivos). Se
embolsilla 2n dólares y el estrato azul "invierte" 2n dólares.
Tienen la pelota los 2 subordinados azules y van a buscar cada uno sus subordinados naranja.
Cada miembro azul se embolsilla 2n dólares y el estrato naranja invierte 4n dólares.
Hasta este momento los azules han recibido 2n cada uno y han pagado n dólares al jefe rojo, por lo que su "ganancia" es de n dólares.
Tiempo después
El jefe rojo ha ganado 2n dólares y los del último nivel (los menos vivos) han pagado cada uno n dólares y no han recibido ni un centavo, y los intermediarios (siempre ellos) han ganado cada uno n dólares.
Cálculos de interés
Nivel Miembros del nivel Total miembros involucrados
0 1=20 1= 20
2 4=22 7= 22+1 - 1
.
.
.
n 2n 2n+1 - 1
Pregunta Nº 1
¿Si en la ciudad de Loja (Ecuador) hay 220000 habitantes, entonces cuántos niveles (rojos, azules, naranjas, verdes, morados, etc.) completos se pueden lograr?
2n+1 - 1 = 220000
2n+1 = 220001
(n+1)ln(2)=ln(220001)
n+1 = ln(220001)/ln(2)
n = ln(220001)/ln(2) - 1 ==> 16 niveles completos
Pregunta Nº 2
¿Cuántas personas se quedan en el último nivel y sin posibilidad de recuperar su dinero?
Respuesta = 2n= 216=65536
Pregunta Nº 3
¿Cuántas personas están involucradas en el juego?
2n+1 - 1 = 131071
Pregunta Nº 4
¿Si la cantidad que se cobra a cada "súbdito" es de $1000, cuánto pierden los del último nivel?
Repuesta = 65 millones 535 mil
Pregunta Nº 5
¿Para trabajar con 17 niveles completos cuántas personas deben involucrarse en el juego?
2n+1 - 1 = 262143
Pregunta Nº 6
¿Cómo funciona, para el caso de 3 subordinados?
Nivel Miembros del nivel Total miembros involucrados
0 1= 30
1 3= 31
2 9= 32
3 27= 33
4 81= 34
5 243= 35 30 + 31 + 32 + 33 + 34 + 35
.
. Serie geométrica de razón 3
3 27= 33
4 81= 34
5 243= 35 30 + 31 + 32 + 33 + 34 + 35
.
. Serie geométrica de razón 3
.
n 3n 1*(1-3n+1)/(1-3)= (3n+1-1)/2
Pregunta Nº 7
Pregunta Nº 7
Si en la ciudad de Loja (Ecuador) hay 220000 habitantes, entonces cuántos niveles completos se pueden lograr?
(3n+1-1)/2 =220000
(3n+1-1) =440000
3n+1 = 440001
(n+1)ln(3) = ln(440001)
n = ln(440001)/ln(3) -1
n = 10.8281 ==> 10 niveles
Pregunta Nº 8
¿Cuántas personas se quedan en el último nivel y sin posibilidad de recuperar su dinero?
Respuesta = 3n= 310= 59049
Pregunta Nº 9
¿Si la cantidad que se cobra a cada "súbdito" es de $1000, cuánto pierden los del último nivel?
Repuesta = 59 millones 49 mil
Pregunta Nº 10
¿Para trabajar con 11 niveles completos cuántas personas deben involucrarse en el juego?
(3n+1-1)/2 =265720
Pregunta Nº 11
¿Si en Ecuador hay 14 millones de adultos, entonces cuántos niveles completos se pueden lograr?
(3n+1-1)/2 = 14000000
(3n+1-1) = 28000000
3n+1 = 28000001
(n+1)ln(3) = ln(28000001)
n = ln(28000001)/ln(3) -1
n = 14.6085 ==> 14 niveles
Pregunta Nº 12
¿Cuántas personas se quedan en el último nivel y sin posibilidad de recuperar su dinero?
Respuesta = 314= 4782969
Pregunta Nº 13
¿Si la cantidad que se cobra a cada "súbdito" es de $1000, cuánto pierden los del último nivel?
Repuesta = 4 mil setecientos ochenta y dos millones 969 mil
Pregunta Nº 14
¿Para trabajar con 15 niveles completos cuántas personas deben involucrarse en el juego?
(3n+1-1)/2 =21523360
Problema Nº 14
Maestro Mate
Si un bachiller recomienda el blog a dos personas y éstos a dos y así sucesivamente, para un universo de 220 mil bachilleres, ¿Cuántos niveles se requieren.
Pequeño capitán es el mismos caso de Loja, se requieren 16 niveles.
Problema Nº 15
En cierto mes hubo tres martes que correspondieron a días con número par. ¿Qué día de la semana correspondió al 21 de ese mes?
Solución
Los martes que correspinden a días pares son: 2, 16, 30, por tanto el día 21 es domingo.
Problema Nº 16
Una persona compra cierto número de trajes por $20500, vendió una parte por $15000, cobrando por cada traje lo mismo que le costaron. Hallar el número de trajes que le quedan, para el caso de precio máximo de compra.
Solución
Como vende un lote en 15000, basta con hacer un tabla de unidades vendidas por precio que será el mismo de compra
Unidades vendidas Total venta Precio unitario
1 15000 15000/1
2 15000 15000/2
3 15000 15000/3
.
.
.
n (n es natural) 15000 15000/n
Ahora conociendo el precio de venta = 15000/n, corresponde buscar las unidades compradas.
Unidades compradas = Total compra/precio = 20500(/15000/n) = (205/150)*n = (41/30)*n
Para que la condición que el precio sea máximo se cumpla, las unidades compradas (41/30)*n) deben ser mínimas y por tanto n debe ser mínimo -y por supuesto natural- entonces ==> n=30
Por tanto unidades compradas = 41
Unidades vendidas =n = 30
___
Restantes 11
Nota: para valores de n =60, 90, ...30k podrían ser soluciones si no hubiere la condición de precio máximo.
Problema Nº 17
Para los números naturales p & q se define la operación
Análisis caso II
Si p es impar entonces p = 2k-1
Si q es par entonces q=2n
P*k = (2k-1)*2n + 2k-1
P*k = 4kn -2n + 2k -1
= 2(2kn-n+k)-1 = 2s - 1 ==> p*q es impar
Los martes que correspinden a días pares son: 2, 16, 30, por tanto el día 21 es domingo.
Problema Nº 16
Una persona compra cierto número de trajes por $20500, vendió una parte por $15000, cobrando por cada traje lo mismo que le costaron. Hallar el número de trajes que le quedan, para el caso de precio máximo de compra.
Solución
Como vende un lote en 15000, basta con hacer un tabla de unidades vendidas por precio que será el mismo de compra
Unidades vendidas Total venta Precio unitario
1 15000 15000/1
2 15000 15000/2
3 15000 15000/3
.
.
.
n (n es natural) 15000 15000/n
Ahora conociendo el precio de venta = 15000/n, corresponde buscar las unidades compradas.
Unidades compradas = Total compra/precio = 20500(/15000/n) = (205/150)*n = (41/30)*n
Para que la condición que el precio sea máximo se cumpla, las unidades compradas (41/30)*n) deben ser mínimas y por tanto n debe ser mínimo -y por supuesto natural- entonces ==> n=30
Por tanto unidades compradas = 41
Unidades vendidas =n = 30
___
Restantes 11
Nota: para valores de n =60, 90, ...30k podrían ser soluciones si no hubiere la condición de precio máximo.
Problema Nº 17
Para los números naturales p & q se define la operación
P*q
= p.q
+ p
Dadas las condiciones,
I. p es par
II. p es un número impar y q un número
par
III. p es impar y q número impar
Diga en cada caso si el resultado de p*q es par o impar
Solución
Análisis caso I
Si p es par entonces p = 2k
p*k = p.q +p = 2k.q + 2k = 2(kq +2) = 2m ==> p*q es par
Análisis caso I
Si p es par entonces p = 2k
p*k = p.q +p = 2k.q + 2k = 2(kq +2) = 2m ==> p*q es par
Análisis caso II
Si p es impar entonces p = 2k-1
Si q es par entonces q=2n
P*k = (2k-1)*2n + 2k-1
P*k = 4kn -2n + 2k -1
= 2(2kn-n+k)-1 = 2s - 1 ==> p*q es impar
Análisis caso III
p es impar ==> p = 2k-1
q es impar ==> q= 2s-1
P*k = (2k-1)*(2s-1) + 2k-1
= 4ks – 2k – 2s +1 +2k -1
= 4ks – 2s = 2(2ks-s) = 2m ==> p*q = par
Problema Nº 18
Sea f(x)= p+qsen(kx)
Con:
Período 4π
Máximo
= 11
Mínimo
= 3
Hallar p,q & k
Hallar p,q & k
Solución:
El mínimo de f(x) sucede cuando sucede el de sen(x) (que = -1)
p+q(-1)=3
El máximo sucede cuando sucede el de sen(x) (que es = 1)
p+q=11
Entonces queda el sistema
p - q =3
p + q = 11
==> p=7 & q=4
Usando la propiedad del período f(x)=f(x+P)
p+qsen(kx)=p+qsen[k(x+4π)]
sen(kx)=sen[k(x+4π)]
sen(kx)=sen(kx)*cos(k4π) + cos(kx)*sen(k4π)
Para que satisfaga la igualdad
Cos(k4π)=1
Cos(k4π)=1
Sen(k4π)=0
k4π=2π (el mínimo valor que satisface la condición)
k4π=2π (el mínimo valor que satisface la condición)
K=1/2
Problema Nº 18
Los
esposos Hilda y Javier tienen 4 hijos. Alfonso es hijo del hijo de Javier.
Pamela es hija de la hija de Hilda . Si los otros 2 hijos de Hilda y Javier son
Mariela y Jorge, y cada uno tiene dos hijos ¿cuantos primos en total tiene los
hijos de Mariela
Solución
Problema Nº 19
En una fábrica de pizarras cada empleado puede hacer, en una hora, dos pizarras grandes o treinta cinco pequeñas. Si la fábrica dispone de tres horas para producir un pedido de veinte pizarras grandes y setecientas pequeñas...¿Cuántos empleados, como mínimo, debe tener para cumplir con el pedido?
Solución:
Matemáticamente
Obreros para las pizarras pequeñas = 700/(3*35) = 6.67 que significan 7
grandes = 20/(3*2 = 3.33 que significan 4
Entonces matemáticamente se requieren 10 obreros pero en la vida real 11.
Entonces el mínimo es de 10 obreros y el problema está en analizar como hacer el pedido con ellos
4 obreros trabajan haciendo pizarras pequeñas un tiempo de 20/(4*2)=2.5 horas, entonces la media hora restante la invierten en fabricar (.5)*4*35 = 70 pizarras grandes.
Los 6 obreros restantes trabajan 3 horas fabricando pizarras pequeñas = 6*3*35 = 630, que acumuladas con las 70 da un total de las 700 pequeridas.
Problema Nº 20
Un tren sale de San José con cierto número de personas. En la primera parada la mitad abandona el tren y sube uno. En la segunda parada un tercio abandona el tren y sube un pasajero, con lo cual en el tren quedan 15 pasajeros... ¿Cuántos pasajeros abordaron el tren en San José?
Solución
Sea X el número de pasajeros que parten de San José.
Primera parada
La mitad abandona el tren y sube uno.
La mitad que queda es X/2 y sube 1, por tanto en el tren hay (X/2) + 1
Entonces van rumbo a la segunda parada (X/2) + 1
Segunda parada
En la segunda parada un tercio abandona el tren y sube uno
Como un tercio abandona el tren, lógicamente en él quedan dos tercios
Quedan (2/3)*[(X/2) + 1)] pero como sube un pasajero en total quedan
(2/3)*[(X/2) + 1)] +1 y esa cantidad es igual a 15, entonces finalmente es
(2/3)*[(X/2) + 1)] +1 = 15
(2/3)*[(X/2) + 1)] = 14
[(X/2) + 1)] = (3/2)*14
[(X/2) + 1)] = 21
(X/2) = 21 - 1
X/2 = 20
X = 40
Problema Nº 21
Se ha planteado un examen de n preguntas, todas con el mismo valor de puntuación, de las que un alumno ha respondido correctamente 15 de las 20 primeras preguntas y responde correctamente un tercio de las preguntas restantes. Si la calificación del alumno es 5 sobre 10 ¿Cuántas preguntas tenía el examen?
Solución:
Sea n la cantidad total de preguntas, entonces:
Primer bloque: 20 preguntas
Bloque restante: n-20
Puntaje obtenido en el primer bloque: 15*10 + 5*0 = 150
Puntaje obtenido en el segundo bloque: [(n-20)/3]*10 + [(n-20)2/3]*0 = [(n-20)/3]*10= [(n-20)/3]*10
Total de notas = {150 + [(n-20)/3]*10}
Promedio = {150 + [(n-20)/3]*10} / n = 5
Entonces: {150 + [(n-20)/3]*10} = 5n
150*3 + 10n - 200 = 15n
450 - 200 = 5n
250 = 5n ==> n =50
Problema Nº 22
Dado un número natural n, determinar cuánto le falta para convertirse en múltiplo de:
- 6
- 12
- de 6 y 12
Solución:
1.
a = resto(n;6) es el resto de dividir n entre 6. Ejemplo a = resto (50;6) = 2, lo que quiere decir que 50 = 8*6 + 2 donde se observa que a n en este caso 50 le falta 6 - 2 = 4 para ser múltiplo de 6, o sea el próximo múltiplo es 50 + 4 = 54. En general lo que le falta a un número para llegar al próximo múltiplo es número del cual es múltiplo menos el resto.
Entonces al número n le faltan 6 - a ó 6 - resto(n;6) para llegar a ser múltiplo de 6.
2.
b = resto(n;12) es el resto de dividir n entre 12. Ejemplo b = resto (52;12) = 4, lo que quiere decir que 52 = 4*12 + 4 donde se observa que a n (en este caso 52) le falta 12 - 4 = 8 para ser múltiplo de 12, o sea el próximo múltiplo es 52 + 8 = 60.
En general al número n le faltan 12 - b ó 12 - resto(n;12) para llegar a ser múltiplo de 12.
3.
Si el número n es múltiplo de 12, entonces es múltiplo de 6, por lo siguiente:
n = k*12, donde k es un número natural, pero 12 = 6*2 por lo que n = k*2*6 = 6*(k*2) lo que implica que es múltiplo de 6.
Ahora bien, para que n sea múltiplo de 6 & 12, basta que sea múltiplo de 12 por lo que para a n le falta para ser múltiplo de 6 & 12 es lo siguiente: 12 - resto(n;12)
Si el número n es múltiplo de 12, entonces es múltiplo de 6, por lo siguiente:
n = k*12, donde k es un número natural, pero 12 = 6*2 por lo que n = k*2*6 = 6*(k*2) lo que implica que es múltiplo de 6.
Ahora bien, para que n sea múltiplo de 6 & 12, basta que sea múltiplo de 12 por lo que para a n le falta para ser múltiplo de 6 & 12 es lo siguiente: 12 - resto(n;12)
Problema Nº 23
Dado un número natural n, determinar cuánto le falta para convertirse en múltiplo de 6 pero no de 12.
Solución:
Si el número n es múltiplo de 6 entonces n = j*6, para j perteneciente a los naturales n, j puede ser par o impar.
j = 2*k para el caso que j sea par, k pertenece a N
j = 2*k -1 para el caso que j sea impar, k pertenece a N
Para el caso que j sea impar, n = j*6 ó n = (2*k - 1)*6 = 12*k - 6, lo que implica que el resto de dividir n entre 6 es -6. Entonces si n = j*6 para j impar, n es múltiplo de 6 pero no de 12.
Lo que falta a n para ser múltiplo de 6 es 6 - resto(n;6), por lo que np = n + 6 - resto(n;6)
Ahora si el resto(np/6;2) es 1 significa que np es múltiplo de 6 y no de 12,
y si el resto(np/6;2) es 0, significa que np es múltiplo de 6 y de 12, por lo que el próximo múltiplo de 6 y de 12 es = np+6.
Dos ejemplos:
Primero
Sea n = 37
Resto(37;6) = 1
Faltante para llegar al próximo múltiplo de 6 = 6 - 1 = 5
np = 37 + 5 = 42
Resto(42/6;2) = 1, como el resto es 1 entonces 42 es múltiplo de 6 pero no de 12.
Segundo
Sea n = 46
Resto(46;6) = 4
Faltante para llegar al próximo múltiplo de 6 = 6 - 4 = 2
np = 46 + 2 = 48
¿Es np múltiple de 12?
Resto(48/6;2) = 0, como el resto es 0 entonces 48 es múltiplo de 6 y de 12.
Solución:
Si el número n es múltiplo de 6 entonces n = j*6, para j perteneciente a los naturales n, j puede ser par o impar.
j = 2*k para el caso que j sea par, k pertenece a N
j = 2*k -1 para el caso que j sea impar, k pertenece a N
Para el caso que j sea impar, n = j*6 ó n = (2*k - 1)*6 = 12*k - 6, lo que implica que el resto de dividir n entre 6 es -6. Entonces si n = j*6 para j impar, n es múltiplo de 6 pero no de 12.
Lo que falta a n para ser múltiplo de 6 es 6 - resto(n;6), por lo que np = n + 6 - resto(n;6)
Ahora si el resto(np/6;2) es 1 significa que np es múltiplo de 6 y no de 12,
y si el resto(np/6;2) es 0, significa que np es múltiplo de 6 y de 12, por lo que el próximo múltiplo de 6 y de 12 es = np
Resto(42/6;2) = 1, como el resto es 1 entonces 42 es múltiplo de 6 pero no de 12.
Segundo
Sea n = 46
Resto(46;6) = 4
Faltante para llegar al próximo múltiplo de 6 = 6 - 4 = 2
np = 46 + 2 = 48
¿Es np múltiple de 12?
Resto(48/6;2) = 0, como el resto es 0 entonces 48 es múltiplo de 6 y de 12.
Problema Nº 24
En una frutería venden naranjas en las siguientes modalidades:
- $0,20 por unidad
- $1,00 por paquete de 6 unidades
- $1,60 por paquete de 12 unidades
Se pide encontrar el monto a pagar en función de la cantidad de naranjas adquiridas.
Solución:
Sean n las naranjas compradas
Docenas adquiridas
Docenas = cociente(n;12), el cociente de dividir las naranjas adquiridas entre 12. Por supuesto quedará un residuo (rd) que puede ser 0
Medias docenas adquiridas
1/2 docenas adquiridas que se obtienen a partir del resto de las docenas
Medias_docenas = cociente(rd;6), el cociente de dividir el resto (rd) de las docenas adquiridas entre 6. Por supuesto quedará un residuo (rmd) que puede ser 0
Unidades
El residuo rmd que arroja la obtención las medias docenas
Monto a pagar:
Docenas adquiridas
Docenas = cociente(n;12), el cociente de dividir las naranjas adquiridas entre 12. Por supuesto quedará un residuo (rd) que puede ser 0
Medias docenas adquiridas
1/2 docenas adquiridas que se obtienen a partir del resto de las docenas
Medias_docenas = cociente(rd;6), el cociente de dividir el resto (rd) de las docenas adquiridas entre 6. Por supuesto quedará un residuo (rmd) que puede ser 0
Unidades
El residuo rmd que arroja la obtención las medias docenas
Monto a pagar:


















No hay comentarios:
Publicar un comentario