La función exponencial y las curvas de contagio COVID en Ecuador

Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
29 abril 2020
Problema Nº 1
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año?
Solución:
Debe pagar el capital más los intereses generados.
Intereses
No es más que sacar el 8% del capital = capital*i +200,00*8/100 = 200,00*,08 = 16
Total a pagar = 200,00 + 16 = 216
Total a pagar = capital + intereses = capital + capital*i = capital*(1 + i) = c*(1+i)
Problema Nº 2
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año si los intereses se capitalizan semestralmente?
Solución:
Ahora por simple regla de tres el interés será la mitad de i para cada semestre.
Al final del primer semestre:
Total a pagar = capital + intereses = capital + capital*i = capital*(1 + i/2) = c*(1+i/2)
El segundo semestre ahora arranca con un nuevo capital = c*(1+i/2) = C1 que al final, del semestre y año, será C2 = C1*(1+i/2) = c*(1+i/2)*(1 + i/2) = c*(1+i/2)2 = 200,00*(1 + 0,08/2)2 = 216,32
Problema Nº 3
Total a pagar = c*(1+i/24)24 = c*(1+0,08/24)24 = 216,628592
Problema Nº 5
Al final del primer semestre:
Total a pagar = capital + intereses = capital + capital*i = capital*(1 + i/2) = c*(1+i/2)
El segundo semestre ahora arranca con un nuevo capital = c*(1+i/2) = C1 que al final, del semestre y año, será C2 = C1*(1+i/2) = c*(1+i/2)*(1 + i/2) = c*(1+i/2)2 = 200,00*(1 + 0,08/2)2 = 216,32
Problema Nº 3
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año si los intereses se capitalizan trimestralmente?
Total a pagar = c*(1+i/4)4 = 200,00*(1 + 0,08/4)4 = 216,486432
Problema Nº 4
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año si los intereses se capitalizan quincenalmente?
Total a pagar = c*(1+i/24)24 = c*(1+0,08/24)24 = 216,628592
Problema Nº 5
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año si los intereses se capitalizan diariamente?
Total a pagar = c*(1+i/365)365 = c*(1+0,08/365)365 = 216,655514
Problema Nº 6
Si usted recibe un préstamo de un capital c de $200,00 al 8% anual cuánto debe pagar luego de transcurrido un año si los intereses se capitalizan en períodos cada vez más pequeños y por ende más numerosos
Solución
Ayudado de una hoja de cálculo se nota la estabilización del pago cuando los períodos (en este caso n) crecen y se acercan al infinito
Entonces trabajando con tres decimales la respuesta bien podría ser 216,657.
Problema Nº 7
Si al finalizar cada año se renueva el crédito con lo recaudado, capitalizando cada instante, entonces cuánto se recaudaría al final del décimo año?
Solución:
Utilizando el método del problema 6 se obtiene que al final del décimo año lo recaudado por el prestamista será 445,108.
Obtener la gráfica de lo recaudado por año
- La gráfica es lineal?
- Exponencial?
- Logarítmica?
- Potencial?
Solución:
Por ahora se puede afirmar que la curva no es lineal
Truco
Se puede achatar verticalmente la curva para que parezca lineal. Nada ético cuando de información se trata.
Se puede achatar verticalmente la curva para que parezca lineal. Nada ético cuando de información se trata.
Problema Nº 9
Considerando el capital inicial y los valores de la última fila durante los últimos diez años existe una relación entre ellos?
Solución
Todo número actual es igual al anterior multiplicado por la misma constante. 1,083287 es la constante en este caso.
Problema Nº 10
Todo número actual es igual al anterior multiplicado por la misma constante. 1,083287 es la constante en este caso.
Problema Nº 10
¿Lo deducido en el problema 9 es una característica de la función exponencial?
Solución
Sí
Todo número actual es igual al anterior multiplicado por la misma constante.
Problema Nº 11
Defina una función para obtener lo acumulado al final de un enésimo año y hacer gráficas para 30 y 100 años.
Una función exponencial.
Problema Nº 12
La leyenda del ajedrez
Coloque 1 grano de trigo en la primera casilla, 2 en la segunda, 4 en la tercera, 8 en la cuarta y así sucesivamente hasta colocar todos los granos. Si cada grano pesa un gramo y un camión trailero carga 4o toneladas entonces cuántos camiones se requieren para transportar los granos depositados en la última casilla?
Solución
Cantidad de granos = 2n-1 = 264-1 = 263 = 9,22337* 1018 granos y gramos a la vez que si se divide entre 40*1000*1000 (4o toneladas que carga cada camión) se tendrá el número de camiones traileros = 23.058.400.000.000.000 Problema Nº 13
Calcular la cantidad de granos depositado en cada una de las primeras 24 casillas y el total depositado en el tablero.
En el tablero se han colocado 16.777.215 granos de trigo
Problema Nº 14
Asumiendo que tiene una larga lista con 1.000.000 de nombres, ordenadas alfabéticamente, de páginas web, cuántos pasos, como máximo, le llevaría encontrar un nombre?
Un paso consiste en picar la lista en la mitad y desechar el pedazo que no contiene el nombre buscado. Al método se lo denomina búsqueda binaria.
En el tablero se han colocado 16.777.215 granos de trigo
Problema Nº 14
Asumiendo que tiene una larga lista con 1.000.000 de nombres, ordenadas alfabéticamente, de páginas web, cuántos pasos, como máximo, le llevaría encontrar un nombre?
Un paso consiste en picar la lista en la mitad y desechar el pedazo que no contiene el nombre buscado. Al método se lo denomina búsqueda binaria.
Problema Nº 15
Igual que en el problema 14 pero para una lista de 20.000.000.000 (veinte mil millones) de páginas.
Igual que en el problema 14 pero para una lista de 20.000.000.000 (veinte mil millones) de páginas.
Solución
Hacer una lista gráfica como en el problema anterior ya no es procedente por lo que toca buscar la cantidad de pasos matemáticamente
2n ≥ 1.000.00.000
nlog(2) ≥ log(1.000.000.000)
com0 log(2)>0
n ≥ log(1.000.000.000)/log(2)
n ≥ 29,90 è n =30
SEGUNDA PARTE: Coronavirus
Muchos ciudadanos, entre ellos académicos, médicos, epidemiólogos, matemáticos y más hierbas, expresan que el contagio del virus es exponencial y que cada persona contagiada contagia a dos personas a su vez. Esta situación puede verse gráficamente.
Se puede observar que en el ejemplo hay 5 niveles: 0, 1, 2, 3, 4, donde la cantidad de contagiados por nivel es 2n
Niveles = 0, 1, 2, 3, 4 en total son 5
Cantidad de infectados = 1 + 2 + 4 + 8 + 16 = 31
Donde los niveles pueden ser: contactos, horas, días
Problema Nº 16
Si la población Guayas es 4.387.434 entonces cuántos eventos se requieren para contagiar a todos asumiendo que el contagio es exponencial?
En 22 días se cubre todo Guayas y en 23 todo Ecuador del Carchi al Macará
Truco
Asumiendo que lo anterior es cierto en lo que respecta al modelo de contagio se puede aplanar la curva para no asustar muchos
Problema Nº 17
Si la población del globo es de 7.700.000.000 hab. entonces de acuerdo al modelo anterior en cuántos niveles se contagiará toda la población?
En el nivel 32 todo el mundo contagiado.
Quizá sea el momento para calcular el acumulado de contagiados en todos los niveles con una fórmula
Sea Sn la suma de todos los niveles
Sn = a0 + a0*r + a0*r2
+ a0*r3 + a0*r4 + … + a0*rn-2
+ a0*rn-1 + a0*rn (1)
Si a todos los términos los multiplicamos por la razón r
Sn*r
= a0*r + a0*r2
+ a0*r3 + a0*r4 + …+ a0*rn-2
+ a0*rn-1 + a0*rn + a0*rn+1 (2)
Restando (1) - (2)
(1-r)* Sn = a0 - a0*rn+1
= a0(1 - rn+1)
Sn = a0(1 - rn+1)/(1-r)
Ahora el problema se reduce a: Dada la sumatoria calcular los niveles.
Sn = a0(1 - rn+1)/(1-r)
(Sn)*(1-r) = a0(1 - rn+1)
[(Sn)*(1-r)]/a0 = 1 - rn+1
rn+1 = 1 - [(Sn)*(1-r)]/a0
(n+1)*log(r) = log{1 - [(Sn)*(1-r)]/a0}
n+1 = log{1 - [(Sn)*(1-r)]/(a0*log(r)}
n = log{1 - [(Sn)*(1-r)]/(a0*log(r)} - 1Para el caso que nos ocupa
r =2
a0 = 1
S = 7.700.000.000
n = log(7.700.000.000 - 1)/log(2)n = 31,84
El inmediato valor de n (que debe ser entero) es 32,
Problema Nº 18
Obtener la data de contagios de Guayas de la página oficial
- Resalte el área de interés
- Copiar (para luego pegar)
- Pegar (con pegado especial) con texto unicode en excel por ejemplo.
Data publicada el 01/5/2020
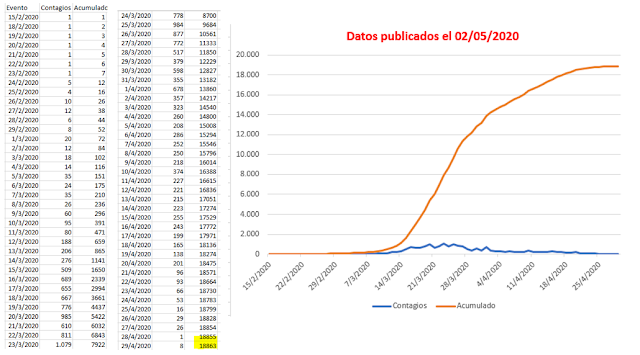
Data publicada el 02/5/2020
Problema Nº 19
Cómo fue distribuida la diferencia de 1057 contagiados entre el 01/05/2020 y el 02/05/2020?
Un poquito aquí, un poquito allá, y si a la curva le sale un "pupo", como posiblemente en el 27/04/2020, pues quitan un poco de datos y se los llevan a otro lado quizá para tapar, a la vieja usanza cual hojalatero, un hueco en el 24/4/2020 y así emparejar o darle un peralte suave a la curva para que no asuste mucho.
Problema Nº 20
Cómo fue distribuida la diferencia de 2074 contagiados entre el 02/05/2020 y el 03/05/2020?
Usando la misma técnica del hojalatero aplicada en el problema 19. A todas las fechas marcadas en rojo les esquilmaron un poco de datos pa'llevarlos a otro sitio dentro de la misma curva.
Problema Nº 21
Y cuál es la idea de lo hecho en los problemas 19 y 20?
Nada más y nada menos que un PQC (Para Que Cuadre) y que se vea como que la curva se va aplanando y aunque tenga esta forma
presentarla como la siguiente en la página oficial
pero que en ningún momento representan la realidad al ser modificada, hacia atrás, día a día. Bajo esas condiciones no se podrá conseguir las curvas de contagio y menos la exponencialidad que algunos expertos pregonan sin mostrar argumentos. Un gran daño para futuros estudios epidemiológicos.
TERCERA PARTE: Analizando las curvas de Guayas que presentan las páginas oficiales.
En edición






















No hay comentarios:
Publicar un comentario