5. Áreas y Perímetros

Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
11 marzo 2014


Problema Nº 1 

El perímetro de un rectángulo es 18 y su área es 20. ¿Cuáles son las dimensiones del rectángulo?

b = base
a = altura

Entonces

2a+2b = 18  ==> a + b = 9 ==> b = 9 -a

a.b = 20 ==> a(9-a)=20 ==>  a²-9a+20=0 ==> (a-5)*(a-4)=0 ==> a =5 & b= 4 (o viceversa)

Si a=5 ==> b = 9 - a ==> b = 4



Problema Nº 2 

En un rectángulo de perímetro 40, la diferencia entre la base y la altura es 2. ¿Cuál es el área?

b = base
a = altura

Entonces

2a+ab = 40 ==> a + b = 20
a - b = 2

Resolviendo

a = 11
b = 9

Área = 99


Problema Nº 3

Si el cuadrado inscrito al círculo tiene un lado de dimensión 2a calcular el área roja. 

El radio r es la hipotenusa del triángulo por tanto  r²=a²+a² 

Como el área de círculo es Πr², entonces, área = Π(a²+a²) =  Π(2a²) 

El área del cuadrado es lado²,  por tanto área = (2a)² = 4a² 

El área roja es área del círculo - área del cuadrado =  Π(2a²) - 4a² = 2a²(Π - 2)

Problema Nº 4

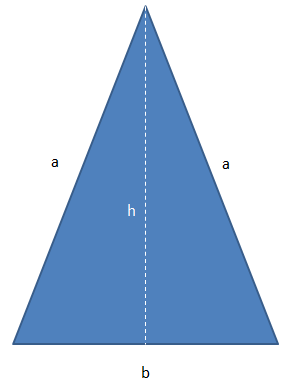
El área de un cuadrado de lado L es igual a dos veces el área de un triángulo de base L. ¿Cuál es la altura h del triángulo?

Área del cuadrado = L²

Área del triángulo = (Lh)/2, por tanto L²= 2(Lh/2) ==>L = h. La altura del triángulo es L.


Problema Nº 5

Demostrar que el área de un rombo es igual a (diagonal menor x diagonal mayor)/2

Observar que la diagonal mayor es 2b y la menor es 2a

Problema Nº 6

Demostrar que el área del paralelepípedo es bh (base x altura)

Problema Nº 7

Obtener el área sombreada del círculo de radio = r

Todo el perímetro del círculo (2Πr) encierra un área de Πr².

Trabajando con radianes
 
1. Determinar cuál es la porción de perímetro del área sombreada, que
    corresponde a 15º (=90º-30º-45º)

    Primera regla de tres
 
   2Πr     --------> 360º
    X       -------->  15º

    X = (2Πr)*15/360 = Πr/12


2. Determinar el área sombreada.

   Segunda regla de tres

   2Πr  ------> área completa(Πr²)

   Πr/12 ------>    X

  X = (Πr²)(Πr/12)/(2Πr)

  X = Πr²/24


Trabajando con grados

360º -------> Πr²

15º ---------> X


X= Πr²*15/360 =

X = Πr²/24


Problema Nº 8

Obtener el área roja

Solución:

1. Determinar el radio del círculo azul

    Es la mitad del lado del primer cuadrado = 2/2 = 1

2. Determinar el lado y área del cuadrado rojo

    La diagonal del cuadrado rojo es dos veces el radio del círculo azul = 2
    
    Con este dato se obtiene el lado del cuadrado rojo

    diagonal² = l²  +  l²
  
    2²  = 2l²

    2 = l²
     l = SQRT(2) 

    Nota: SQRT significa Raíz Cuadrada
 
    Área del cuadrado rojo = l² = 2

3. Determinación del área del círculo blanco.

   Radio = l/2

4. Determinación del círculo blanco

   Área =  Πr²  =  Πl²/4   = Π/2 

5. Área solicitada

   Área del cuadrado rojo - la del círculo blanco

   = 2 - Π/2

 

Problema Nº 9
 
El perímetro de un trapecio isósceles es de 98 m, las bases miden 48 y 40 m respectivamente. Calcular los lados no paralelos y el área.

 Solución:

1. Cálculo de los lados no paralelos

   l + 40 + l + 48 = 98 ==> l = 5

2. Cálculo del área

 

    2.1. Cálculo de h

         h² + 4² = 5² 

         h = SQRT(25-16) =3

    2.2. Cálculo del área del triángulo

         Área triángulo izquierdo = (4)(3)/2 = 6

3. Cálculo del área total

   Área total = área triángulo izquierdo + área del rectángulo central + área triángulo derecho

   Área total = 6+120+6 = 132 m² 

  
Forma alternativa

Área = ((base inferior + base superior)/2)(altura) = (88/2)*3 =  44*3= 132 m²

 
 

Problema Nº 10
 
Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio r.

Solución: Cálculo de la altura h  r = (2/3)h ==> h = (3/2)r L2 = (L/2)2 + h2    L2 = (L/2)2 + ((3/2)r)2        (3/4)L2 = (9/4)r2  L2 =  3r2 Área del triángulo = 2 veces el área del triángulo izquierdo = 2 (L/2)h/2 Área = Lh/2 = SQRT(3r2)(3/2)r/2        = [SQRT(3)]*(3/4)*r2     Problema Nº 11   Dos veces el área de un cuadrado de lado L es igual a cuatro veces el área de un triángulo de altura L. ¿Cuál es la base del triángulo?  Solución:   Área del cuadrado =L2 Área de triángulo  = b*L/2 Área del cuadrado = 4xÁrea del triángulo L2 = 4(b*L/2) ==> L = 2b ==> b = L/2 Problema Nº 12   Si el lado de un cuadrado es 2 cm más largo que el de otro cuadrado y las áreas de los cuadrados difieren en 36 centímetros cuadrados ¿Cuànto miden los lados de cada uno de ellos? Solución: L = lado del cuadrado más pequeño Área del cuadrado pequeño = L*L Para el cuadrado más grande Lado = L+2 Área del cuadrado grande = (L+2)*(L+2) Área del cuadrado grande - Área del cuadrado pequeño = 36 (L+2)*(L+2)-L*L=36 ==> L2 + 4L + 4 - L2 = 36 ==> 4L = 32 ==> L = 8 Lado = 8 &  Lado = 10 Problema Nº 13   Si en la parte baja de un triángulo equilátero, de lado L y altura H, se inserta un trapecio de altura H/10. Se pide calcular el área de este trapecio y qué fracción es del área del triángulo.   El área del trapecio es (19LH)/(200) = (19)(HL/2)/100 = (19/100)*(HL/2) = (19/100)área del triángulo.  Problema Nº 14     Hallar el área de un triángulo equilátero de lado L. Solución: El área total es dos veces el área del triángulo izquierdo Área del triángulo izquierdo = [(L/2)*H]/2 Se trata ahora de conseguir el valor de la altura H en función del lado L Por Pitágoras  L2 = (L/2)2 + H2  Por tanto: H = SQRT(L2 - (L/2)2)                 H = SQRT(L2 - L2/4)                H = (L/2)*SQRT(3) Área del triángulo izquierdo = (L/2)*(L/2)*SQRT(3)/2 Área del triángulo equilátero = (L2/4)SQRT(3) Problema Nº 15     Hallar el área de un triángulo equilátero, si el segmento que une los puntos medios de los lados mide x unidades. Solución: Suficiente con conseguir el lado L en función del valor X dado y luego aplicar la fórmula del problema 14. Por la ley de la proporcionalidad razón verde = razón roja (L/2)/(X/2) = L/(L/2) L/X = 2 ==> L = 2X Como área del triángulo equilátero = (L2/4)SQRT(3) En este caso se obtiene = ((2X)2/4)SQRT(3) = X2*SQRT(3) Problema Nº 16    En la figura 5BD = 2CD BM es la mediana del triángulo ABD Halle la relación entre el área del triángulo ABM y el área del triángulo ABC. Solución: Relación: x/y = 5/2 ==> x= (5/2)Y = 5y/2 1. Se trata de calcular el área de ABC     Área ABC = (y+x)*(2m)/2 = (y+x)*m = (y+5y/2)*m =7ym/2 2. Calcular el área de ABM = Área(ABD)-Área(BDM)    2.1  Área (ABD)= y*(2m)/2=y*m    2.2  Área(BDM) = ym/2    Área(ABM)=ym -ym/2 = ym/2 3. Calcular la relación Área(ABM)/Área(ABC)     Relación pedida = [ym/2]/[7ym/2]=1/7 Problema Nº 17     En una pista de 6 carriles se va a realizar una competencia de 150 metros planos. Definir los puntos de salida en función del ángulo ø y el radio del arco.

Solución: Carril                Radio 1                 36.50+1 metro =37.50 2                 36.50+2          =38.50 3                 36.50+3          =39.50 4                 36.50+4          =40.50 5                 36.50+5          =41.50 6                 36.50+6          =42.50 Longitud del arco Para cubrir los 150 metros se requieren:  84.39+65.61. El segundo sumando corresponde al carril en forma de arco. 2*pi*r    360º (El perímetro o circunferencia total es 2*pi*r) 65.61      X X=(360º)*65.61/(2*pi*r) (con esto se obtiene el ángulo para cada carril)      Problema Nº 18  El perímetro de un cuadrado equivale al perímetro de un triángulo equilátero, si la medida del lado del triángulo equilátero es 16. ¿Cuánto mide el área del cuadrado?   a.-) 48 b.-) 12 c.-) 144 d.-) 169 Solución: Sea L lado del cuadrado, entonces Perímetro del cuadrado = 4L Perímetro del triángulo = 3*16 = 48 Por tanto = 4L = 48 ==> 48/4 =12 Área del cuadrado = L*L = 144 Problema Nº 19 El área de un trapecio es 25 si la base mayor es el doble de la base menor y la altura es un tercio de la base mayor ¿Cuáles son las medidas del trapecio?. Solución Sean M, m y H la base mayor, menor y altura del trapecio, entonces: m =(1/2)M H = (1/3)M  Área = [(M+M/2)/2]*H             = [(3M/2)/2]*(M/3)        = M*M/4         M*M/4 = 25         M*M = 100             M = 10             m =  5             H =  10/3                   Comprobación: Área = [(10+10/2)/2]*(10/3)         = (15/2)*10/3= 150/6=25 Problema Nº 20  Si tiene un rectángulo de 39 de base y 28 de altura. ¿Cuál es la máxima cantidad de puntos que puede colocar, de tal modo que a distancia entre dos puntos consecutivos sea 5?  Solución: 26 Problema Nº 21 Un granjero dispone de 44m de cerca para crear un corral para sus gallinas, utilizará la pared de su casa como parte del corral, cercando tan solo 3 lados, si el lado paralelo a la pared debe ser 4m mayor que el doble de su anchura, cuáles son las dimensiones del corral?  Solución  Sean a lado paralelo a la pared y b el lado perpendicular, por tanto a+b+b=44, es el perímetro a=2b+4, a es mayor en 4 al doble de la anchura Por tanto a+b+b=44 (2b+4)+b+b=44 4b=40 b=10 a= 2b+4=24 Problema Nº 22 Dado un triángulo equilátero de L m de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices. Solución: Se trata de obtener el área 1 que no es más que la tercera parte del círculo. Por tanto si el radio es R, el área buscada es (1/3)*πR2 Área = (1/3)*πR2. Como R = (2/3)H ==>  Área = (1/3)*π((2/3)H)2 = (1/3)*π(4/9)H2 = (1/3)*π(4/9)H2 = (4π/27)H2. Por Pitágoras: L2. = (L/2)2 + H2  H2. = L2 - (L/2)2 = (3/4)L2 Por tanto el área solicitada es (4π/27)H2 = (4π/27)(3/4)L2. 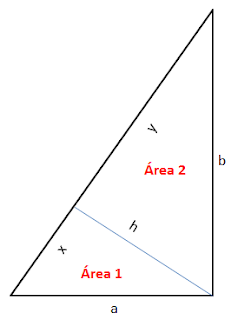= (π/9)L2 Problema Nº 23 Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de D m de diagonal. Solución  Se trata de encontrar la diferencia de dos áreas circulares: El primer círculo (externo) tiene radio D/2 El segundo círculo (interno) tiene radio (D/2))/√2  El área solicitada es π(D/2)2  -  π((D/2))/√2)2 = π(D/2)2(1 - 1/2) = πD2/8   Problema Nº 23 Si los lados no paralelos de un trapecio isósceles se prolongan, quedaría formado un triángulo equilátero de L cm de lado. Sabiendo que el trapecio tiene la mitad de la altura del triángulo, calcular el área del trapecio. Solución H = (L/2)*seno(60º) = (L/2)*√3/2 = (L/4)*√3  D = (L/2)*coseno(60º) = L/4 Área = ((2D + L)/2)H         = ((L/2 + L)/2)(L/4)√3          = L2(1/2 + 1)*(1/8)*√3  = 62(1/2 + 1)*(1/8)*√3  = (36(3/2)/8)*√3          = 108*√3/16  Problema Nº 24 Si B, C, D, H son valores conocidos. Se pide: Área del triángulo azul Área 1 Área 2 Relación entre área1 y área2 Solución: Primero Área = B*H/2 Segundo Área1 = C*H/2 Tercero Área2 = D*H/2 Cuarto Relación de áreas Área1/Área2 = C*H/D*H = C/D Problema Nº 25 Calcular la relación de áreas Área 1 /Área 2 Solución Asumiendo que el área total es 4A, por el ejercicio anterior: Área 2 = 1*A Área 1 = 3*A Entonces Área 1 /Área 2 = 3*A/1A* = 3 Problema Nº 26 Calcular la relación de áreas Área 1 /Área 2 Solución: Entonces Área 1 /Área 2 = 2/1 = 2 Área1 + Área2 = 4 (1) para A = 1 Área 1 /Área 2 = 2 (2) Resolviendo el sistema (1) & (2) 2*Área2 + Área2 = 4 Área2*(3) = 4 Área2 = 4/3 Área1 = 8/3 Problema Nº 27 ¿Si el Área2 es 4/3, entonces cuánto vale el área A3? 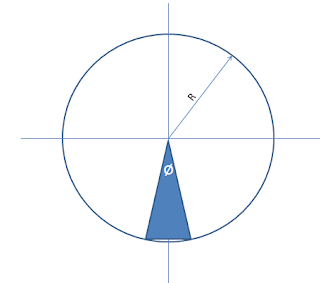Área3 + Área4 = 4/3 (1) Área 4 /Área 3 = 3 (2) Resolviendo el sistema (1) & (2) Área3 + 3*Área3 = 4/3 4*Área3 = 4/3 Área3 = 1/3 Problema Nº 28 Dibujar n triángulos isóceles como el mostrado en la figura y luego demostrar que cuando n tiene a infinito, el área tiende a πR2.    El área del triángulo azul es b*h/2 b = 2*R*seno(ø/2) h = R*coseno(ø/2) Por tanto el área es 2*R*seno(ø/2)*R*coseno(ø/2)/2 = R2*seno(ø/2)*coseno(ø/2)  Pero ø = 2π/n)   Por tanto el área total es n*(R2*seno(ø/2)*coseno(ø/2)) =  n*(R2*seno(π/n)*coseno(π/n)) Nota: seno(x) tiende a x cuando x tiende a 0 n*(R2*seno(π/n)*coseno(π/n)) tiende a n*(R2*(π/n)*1) = πR2. Problema Nº 29 Si el área del triángulo azul es A, cuánto vale el área B. área A = a*h/2 ==> h = 2A/a área B = b*h/2 = b*(2A/a)/2 = b*A/a Problema Nº 30 Encontrar el área del triángulo isóceles Área = b*h/2 Cálculo de h h = SQRT(a2 – (b/2)2)  Problema Nº 31 Encontrar el área del segmento circular, que se encuentra encima de la cuerda AB, de longitud l. El ángulo ACB es ø. Solución Cálculo del área marcada. Paso 1 Si en 2πR (círculo total)  el área es πr2 entonces qué área le corresponde al ángulo ø    Área = ( ø/2π)πR2  Área = ( ø/2)R2  Paso 2 Cálculo del área del triángulo isóceles Área = l*h/2 Cálculo de h h = SQRT(R2 – (l/2)2)  Paso 3 Cálculo del área solicitada Área solicitada =  (ø/2)R2 -l*h/2 = (ø/2)R2  - l*(SQRT(R2 – (l/2)2)/2  Problema Nº 32 Hallar los valores a, b & c del gráfico mostrado Solución a = L - 2L/3 = L/3 b = L - 2L/3 = L/3 c = L - L/3 = 2L/3 Problema Nº 33 Un estanque se llena con un conducción de agua que lo alimenta con una caudal como se ve en la figura: Se pide el agua que ha llegado luego de 7 minutos. Solución  El volumen que llega en el primer minuto es 1M3/minuto*1minuto = 1M3 que no es más que el área de un cuadrilátero de base 1 y altura 1 Volumen luego del primer minuto = 1*1* = 1 Volumen en los minutos [1,2] = 1*2= 2 Volumen en los minutos [2,3] = 1*4= 4 Volumen en los minutos [3,4] = 1*2= 2 Volumen en los minutos [4,5] = 1*2= 2 Volumen en los minutos [5,6] = 1*4= 4 Volumen en los minutos [6,7] = 1*4= 4 En el fondo el volumen de agua ingresado es la suma de áreas = 1 + 2 + 4 + 2 + 2 + 4 + 4 =19 M3   Problema Nº 34 Las longitudes de los lados de un triángulo están en progresión aritmética y las longitudes de sus alturas también están en progresión aritmética. Demostrar que el triángulo es equilátero.  Solución Si la razón r es 0, entonces todos los lados son iguales y el triángulo es equilátero y por ende las alturas son iguales lo que implica x = 0. Si la razón x es 0, entonces todas las alturas son iguales y el triángulo es equilátero y los lados son iguales lo que implica r = 0. Problema Nº 35 En un triángulo rectángulo trazamos la altura que parte del ángulo recto y el triángulo queda dividido en dos triángulos, uno de los cuales tiene el triple de área que el otro. Si la hipotenusa del triángulo original mide 1, ¿cuánto miden sus catetos? Solución Área 1= xh/2 Área 2 = yh/2 área 2/área 1 = 3 ==> (yh/2)/(xh/2) = 3 ==> y = 3X    (1) Además por enunciado: x + y = 1  (2) Resolviendo (1) & (2) x = 1/4  & y = 3/4 Aplicando Pitágoras en cada uno de los triángulos: a2 = x2 + h2  ==> h2 = a2 - 9/16     (3) b2 = y2 + h2  ==> h2 = b2 - 1/16     (4) a2  + b2 = 1  ==> a2  = 1 -  b2   (5) Igualando (3) & (4) ==> a2 - 9/16 = b2 - 1/16   y utilizando (5) se tiene 1 -  b2 - 9/16 = b2 - 1/16 ==> 2b2 = 1/2 ==> b = 1/2  Utilizando (5)   a2 = 1 -  b2 ==> a2  = 3/4 ==> a = SQRT(3)/ 2  Problema Nº 36 Calcular el área del círculo circunscrito a un cuadrado de perímetro P = 8L y la relación de áreas. Solución: Área = πr2 = π2L2   Como perímetro = P = 8L ==>  L = P/8 Área del círculo=  π2(P/8)2 =   π(P)2/32     Área del cuadrado= (2P)(2P) =  4P2  Relación de áreas = (π(P)2/32)/4P2 = π/128