
Esta obra está bajo una licencia Creative Commons Atribución 3.0 Ecuador.
21 marzo de 2017
Ejercicios con videos
Ejercicio 4_1
Determinar el último dígito de la siguiente cédula ecuatoriana:
1 1 0 0 2 9 3 4 5 ?
Nota
La cédula ecuatoriana tiene el último dígito como validador, este dígito es producto de un algoritmo claramente definido y que se puede unívocamente determinar en base a los nueve (9) dígitos precedentes. El algoritmo de explica -justo- en este ejercicio.
Solución
1 1 0 0 2 9 3 4 5
- Tome los números que se encuentran en las posiciones impares (arriba en rojo) y multiplíquelos por 2 para obtener 2, 0, 4, 6 y 10
- Si alguno de ellos es mayor o igual a 10, réstele 9. En este caso obtendrá 2, 0, 4, 6 y 1
- Sume esta serie de números = 2 + 0 + 4 + 6 + 1 = 13
- Tome los números que se encuentran en las posiciones pares y súmelos = 1 + 0 + 9 + 4 = 14
- Sume los resultados de los puntos 3 & 4 = 13 + 14 = 27. Si la suma es múltiplo de 10, el dígito validador es 0 y se deben obviar los pasos siguientes.
- Consiga la inmediata decena que le queda por encima de 27 (resultado de la suma). La decena es 30.
- A la decena obtenida en el punto 6, que es 30, réstele la suma del punto 5 en este caso 30 - 27 = 3, que es el número buscado
Respuesta
1 1 0 0 2 9 3 4 5 3
Ejercicio 4_2
Determinar el dígito faltante de la siguiente cédula ecuatoriana: 1 1 0 0 x 9 3 4 5 3
Recomendación o conducta de entrada
Practicar el ejercicio 4_1
Solución considerando que x es menor a 5
- Separar el último dígito de la cédula ya que es el dígito validador y no entra en juego: 1 1 0 0 x 9 3 4 5.
- Tomar los dígitos que se encuentran en posición impar: 1, 0, x, 3, 5
- Multiplicar los dígitos por 2: 2, 0, 2x, 6, 10
- Asuma que 2x es menor que 10. Esto implica que x es menor que 5, tal como lo expresa la condición previa: x es menor a 5
- A los productos mayores o iguales a 10 restarle 9: 2, 0, 2x, 6, 1 (recuerde que 2x menor que 10)
- Sumar los productos: 2 + 0 + 2x + 6 + 1 = 2x + 9
- Sumar los números que se encuentran en las posiciones pares: 1 + 0 + 9 + 4 = 14
- Sumar los resultados de las dos sumas: 2x + 9 + 14 = 2x + 23
- Hacer una tabla de valores para x menor a 5 y conseguir -si existe- el valor de x que haga que la diferencia con la próxima decena sea -el dígito validador- 3.
Respuesta:
El único valor de x que satisface la condición de validación (dígito validador es 3) es x = 2
1 1 0 0 x 9 3 4 5 3
1 1 0 0 2 9 3 4 5 3
Videos:
En Youtube hacer clic aquí.
En FaceBook hacer clic aquí.
Solución considerando que x es mayor o igual a 5
- Separar el último dígito de la cédula ya que es el dígito validador y no entra en juego: 1 1 0 0 x 9 3 4 5.
- Tomar los dígitos que se encuentran en posición impar: 1, 0, x, 3, 5
- Multiplicar los dígitos por 2: 2, 0, 2x, 6, 10
- Asuma que 2x es mayor o igual que 10. Esto implica que x es mayor o igual a 5, ya que así lo expresa la condición previa: x es mayor o igual a 5
- A los productos mayores o iguales a 10 restarle 9: 2, 0, (2x-9), 6, 1 (recuerde que 2x es mayor o igual a 10)
- Sumar los productos: 2 + 0 + 2x - 9 + 6 + 1 = 2x
- Sumar los números que se encuentran en las posiciones pares: 1 + 0 + 9 + 4 = 14
- Sumar los resultados de las dos sumas: 2x + 14
- Hacer una tabla de valores para x mayor o igual a 5 y conseguir -si existe- el valor de x que haga que la diferencia con la próxima decena sea -el dígito validador- 3.
Como era de esperarse no hay otra respuesta, ya que no hay un valor de x que permita una diferencia de 3 con la próxima decena.
La única solución posible es: 1 1 0 0 2 9 3 4 5 3
Ejercicio 4_3
Determinar la cédula siguiente a 1100293453
Practicar el ejercicio 4_1
Solución
- Descartar el dígito de validación. Queda 110029345
- Obtener la siguiente cédula = 110029345 + 1 = 110029346
- Conseguir el dígito validador
Por tanto la cédula siguiente es 1100293451
Videos:
Videos:
Ejercicio 4_4
Determinar la cédula inmediatamente inferior a 1100293453
Practicar el ejercicio 4_1
Solución
- Descartar el dígito de validación. Queda 110029345
- Obtener la cédula inferior = 110029345 - 1 = 110029344
- Conseguir el dígito validador
Determinar si la cédula 1100293451 es falsa
Practicar el ejercicio 4_1
- Separar el dígito validador (último dígito): 1 1 0 0 2 9 3 4 5
- Multiplicar por 2 a los dígitos que ocupen la posición impar: 2*1, 2*0, 2*2, 2*3, 2*5 = 2, 0, 4, 6, 10
- A los resultados que excedan o sean iguales a 10, restarles 9 ==> = 2, 0, 4, 6, 1
- Sumar los productos: 2 + 0 + 4 + 6 + 1 = 13
- Sumar los dígitos que se encuentran en posición par: 1 + 0 + 9 + 4 = 14
- Sumar los dos resultados: 13+14 = 27
- Determinar cuánto le falta a 27 para llegar a la próxima decena: 3 = dígito validador
- Como el último dígito de la cédula propuesta es 1, entonces la cédula es falsa
Ejercicio 4_6
Solución
El formato es XX CCCCCCC V
XX corresponde a la provincia
CCCCCCC = Cuerpo de la cédula que varía entre 0000001 y 9999999
V = Dígito de validación
Videos:
Ejercicio 4_7
Solución
xy se puede representar como x*10 + y, (tanto como 34 = 3*10+ 4 = 30 +4 = 34)
Entonces xy - 9 = x + y ==> x*10 + y - 9 = x + y ==> 9*x = 9 ==> x = 1.
Entonces cuando x =1, y puede tomar valores sin restricciones para y que puede tomar valores entre [0, 9]
.
Ejemplos
10 - 9 = 1 +0 =1
11 - 9 = 1 + 1 = 2
12 - 9 = 1 + 2 = 3
13 - 9 = 1 + 3 = 4
14 - 9 = 1 + 4 = 5
15 - 9 = 1 + 5 = 6
16 - 9 = 1 + 6 = 7
17 - 9 = 1 + 7 = 8
18 - 9 = 1 + 8 = 9
19 - 9 = 1 + 9 = 10
Ejercicio 4_8
Solución
Pasos, para el natural n
Ejercicio 4_10
Dos hermanitos van a sacar cédula por vez primera en la Provincia de Loja Ecuador, justo el día que se inaugura el sistema de cedulación con prefijos y dígitos validadores. Le asignan los turnos 22 y 23.
¿Qué cédulas les corresponde?
Recomendación o conducta de entrada
Practicar el ejercicio 4_1, 4_7 & 4_8
Primera cédula: 110000022
Segunda cédula: 110000023
Para la primera cédula: 110000022
Solución:
Separar el dígito validador: XY0029345
Determinar los posibles dominios de las variables X, Y
Como los prefijos de las cédulas van desde 01 hasta 24, (XY) significa que X varía desde 0 hasta 2
1) X=0 ==>01, 02, 03, 04, 05, 06, 07, 08, 09, Y varía entre 1 y 9
2) X=1 ==>10, 11, 12, 13, 14, 15, 16, 17, 18, 19, Y varía entre 0 y 9
3) X=2 ==>20, 21, 22, 23, 24, Y varía entre 0 y 4
Multiplicar por 2 y luego sumar los dígitos que están en posición impar XY0029345 (Recordar que no se trabaja con el dígito validador)
XY0029345
Observar que 2*x<10 siempre, por lo que no hay que restarle 9 en ninguno de los casos
2X + 2*0 + 2*2 + 2*3 + 2*5 = 2X + 0 + 4 + 6 + 10 = 2X + 0 + 4 + 6 + 1 = 2X+11
Sumar los dígitos que están en posición par:
Y + 0 + 9 + 4 = Y + 13
Sumar los resultados de las dos sumas: = (2X+11) + (Y + 13) = 2X + Y + 24
Hacer los cálculos independientes para los 3 valores posibles de X
Primera solución:
Trabajar con 2X + Y + 24, para x = 0 ==> que el resultado de las sumas es Y + 24
La diferencia con la próxima decena es 3 (que es lo que se busca) cuando y = 3. Por tanto la solución es X = 0 & Y = 3 y la cédula es:
0300293453
Segunda solución:
Trabajar con 2X + Y + 24, para x = 1 ==> que el resultado de las suma es Y + 26
La diferencia con la próxima decena es 3 (que es lo que se busca) cuando y = 2. Por tanto la solución es X = 1 & Y = 1 y la cédula es:
1100293453
Tercera solución:
Trabajar con 2X + Y + 24, para x = 2 ==> que el resultado de las suma es Y + 28
No hay solución posible, ya que en ningún caso se consigue que el dígito validador sea 3
En Youtube hacer clic aquí.
Solución:
Luego sumando ahora los dígitos en posición par 1 + 0 + 9 + 4 = 14
Ahora sumando los dos resultados: 12 + módulo(2*x,9)+ 14 = 26 + módulo(2*x,9)
Primer método
Nota: módulo(2*x,9) no es más que 2*x - 9 cuando 2*x ≥ 10
Segundo método
Solución:
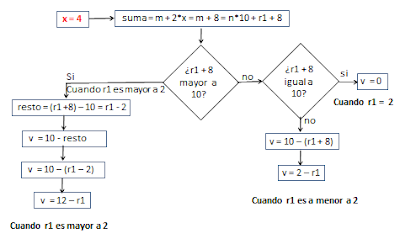
Sea a b c d e f g h x v la cédula donde x es el noveno dígito, y, v el dígito validador.
Tomando los productos 2*a, 2*c, 2*e, 2*g de los dígitos en posición impar excluyendo a x
n1 = módulo(2*a,9) + módulo(2*c,9) +módulo(2*e,9) + módulo(2*g,9)
Entonces n1 es la suma de los productos de aplicar la función módulo a cada uno de dígitos que están en posición impar multiplicados por 2, excluyendo al dígito x.
n2 = b + d + f + h para los dígitos que están en posición par y finalmente
m = n1 + n2
Como m es un número natural se puede descomponer en m = n*10 + r1
Entonces la suma completa que permitirá obtener el validador (v) será:
m + 2*x = n*10 + r1+ 2*x.
De aquí en adelante se analizarán las diferentes casos de valores que vaya tomando la variable x, en la ecuación: n*10 + r1+ 2*x.
Para x = 0
Pregunta:
Solución:
Ejercicio 4_15
Dada la función f siguiente:
A todos y cada uno de los subconjuntos a b c d e f g h x, de la cédula ecuatoriana: a b c d e f g h x v (donde x es un número entero mayor o igual a 0), se le asigna el valor v que es el validador de la cédula donde x está embebido.
Así fue presentado en las redes sociales
¿Cuál es el formato de la cédula ecuatoriana?
El formato es XX CCCCCCC V
XX corresponde a la provincia
CCCCCCC = Cuerpo de la cédula que varía entre 0000001 y 9999999
V = Dígito de validación
Videos:
Ejercicio 4_7
¿En qué caso xy - 9 = x+y, donde xy es número conformado por dos números naturales x e y?
Restricción: Obviamente x es un dígito entre [0,9] e igual para y
Restricción: Obviamente x es un dígito entre [0,9] e igual para y
xy se puede representar como x*10 + y, (tanto como 34 = 3*10+ 4 = 30 +4 = 34)
Entonces xy - 9 = x + y ==> x*10 + y - 9 = x + y ==> 9*x = 9 ==> x = 1.
Entonces cuando x =1, y puede tomar valores sin restricciones para y que puede tomar valores entre [0, 9]
.
Ejemplos
10 - 9 = 1 +0 =1
11 - 9 = 1 + 1 = 2
12 - 9 = 1 + 2 = 3
13 - 9 = 1 + 3 = 4
14 - 9 = 1 + 4 = 5
15 - 9 = 1 + 5 = 6
16 - 9 = 1 + 6 = 7
17 - 9 = 1 + 7 = 8
18 - 9 = 1 + 8 = 9
19 - 9 = 1 + 9 = 10
Ejercicio 4_8
Dado un número natural, encontrar la cantidad que le falta para llegar a la próxima decena. Por ejemplo al natural 237 le faltan 3 para llegar a la próxima decena que es 240.
Pasos, para el natural n
- Dividir n entre 10 y obtener el residuo R
- Hacer la operación 10 - R, que es valor que se busca
Ejemplo:
¿Cuánto le falta a 276 para llegar a la inmediata decena superior?
276/10 ==> Cociente = 27 y residuo = 6, por lo que la cantidad que le falta para la próxima decena es 10 - 6 = 4
Ejercicio 4_9
Determinar el dígito validador de la cédula 110029345X por el método del producto escalar
Recomendación o conducta de entrada
Practicar el ejercicio 4_1, 4_7 & 4_8
Solución
En Youtube hacer clic aquí.
Determinar el dígito validador de la cédula 110029345X por el método del producto escalar
Practicar el ejercicio 4_1, 4_7 & 4_8
Videos:
En Youtube hacer clic aquí.
Ejercicio 4_10
Dos hermanitos van a sacar cédula por vez primera en la Provincia de Loja Ecuador, justo el día que se inaugura el sistema de cedulación con prefijos y dígitos validadores. Le asignan los turnos 22 y 23.
¿Qué cédulas les corresponde?
Practicar el ejercicio 4_1, 4_7 & 4_8
Primera cédula: 110000022
Segunda cédula: 110000023
Para la primera cédula: 110000022
- Se multiplica por 2 a los dígitos de la primera cédula que están en posición impar = 2*1, 2*0. 2*0, 2*0, 2*2
- Se suman los productos de la multiplicación = 2 + 0 + 0 + 0 + 4 = 6
- Se suman directamente los dígitos que están en la posición par = 1 + 0 + 0 + 2 = 3
- Se suman los resultados de los puntos 2 y 3. El resultado es 9
- Se busca el faltante para la próxima decena. El resultado es 1
- Se construye la nueva cédula = 1100000221
- Se multiplica por 2 a los dígitos de la primera cédula que están en posición impar = 2*1, 2*0. 2*0, 2*0, 2*3
- Se suman los productos de la multiplicación = 2 + 0 + 0 + 0 + 6 = 8
- Se suman directamente los dígitos que están en la posición par = 1 + 0 + 0 + 2 = 3
- Se suman los resultados de los puntos 2 y 3. El resultado es 11
- Se busca el faltante para la próxima decena. El resultado es 9
- Se construye la nueva cédula = 1100000239
Ejercicio 4_11
Encontrar los prefijos posibles para la cédula XY00293453
Recomendación o conducta de entrada
Practicar todos los ejercicios anteriores
Encontrar los prefijos posibles para la cédula XY00293453
Practicar todos los ejercicios anteriores
Solución:
Separar el dígito validador: XY0029345
Determinar los posibles dominios de las variables X, Y
Como los prefijos de las cédulas van desde 01 hasta 24, (XY) significa que X varía desde 0 hasta 2
1) X=0 ==>01, 02, 03, 04, 05, 06, 07, 08, 09, Y varía entre 1 y 9
2) X=1 ==>10, 11, 12, 13, 14, 15, 16, 17, 18, 19, Y varía entre 0 y 9
3) X=2 ==>20, 21, 22, 23, 24, Y varía entre 0 y 4
Multiplicar por 2 y luego sumar los dígitos que están en posición impar XY0029345 (Recordar que no se trabaja con el dígito validador)
XY0029345
Observar que 2*x<10 siempre, por lo que no hay que restarle 9 en ninguno de los casos
2X + 2*0 + 2*2 + 2*3 + 2*5 = 2X + 0 + 4 + 6 + 10 = 2X + 0 + 4 + 6 + 1 = 2X+11
Sumar los dígitos que están en posición par:
Y + 0 + 9 + 4 = Y + 13
Sumar los resultados de las dos sumas: = (2X+11) + (Y + 13) = 2X + Y + 24
Hacer los cálculos independientes para los 3 valores posibles de X
Primera solución:
Trabajar con 2X + Y + 24, para x = 0 ==> que el resultado de las sumas es Y + 24
La diferencia con la próxima decena es 3 (que es lo que se busca) cuando y = 3. Por tanto la solución es X = 0 & Y = 3 y la cédula es:
0300293453
Segunda solución:
Trabajar con 2X + Y + 24, para x = 1 ==> que el resultado de las suma es Y + 26
La diferencia con la próxima decena es 3 (que es lo que se busca) cuando y = 2. Por tanto la solución es X = 1 & Y = 1 y la cédula es:
1100293453
Tercera solución:
Trabajar con 2X + Y + 24, para x = 2 ==> que el resultado de las suma es Y + 28
No hay solución posible, ya que en ningún caso se consigue que el dígito validador sea 3
En Youtube hacer clic aquí.
En FaceBook hacer clic aquí.
Ejercicio 4_12
Para la cédula 1 1 0 0 2 9 3 4 x y variar x en el rango [0,9] y ver en qué rango varía la variable y.
Recomendación o conducta de entrada
Practicar todos los ejercicios anteriores
Solución:
Cualquier número natural (como es el caso de las cédulas ecuatorianas) se puede representar por:
Cédula = 10*n+ R1, donde n es un número natural y R1 un natural que toma valores entre [1,9]
También puede representarse por cédula = a + b, donde a & b son naturales y éstos a su vez como: a = 10*m + R2 & b = 10*p + R3.
En general cédula = 10*m + R2 + 10*p + R3 = 10*(m+p) + (R2 + R3), y (R2 + R3) a su vez puede descomponerse si en conjunto suman más de 10.
Cédula = 10*n+ R1, donde n es un número natural y R1 un natural que toma valores entre [1,9]
También puede representarse por cédula = a + b, donde a & b son naturales y éstos a su vez como: a = 10*m + R2 & b = 10*p + R3.
En general cédula = 10*m + R2 + 10*p + R3 = 10*(m+p) + (R2 + R3), y (R2 + R3) a su vez puede descomponerse si en conjunto suman más de 10.
Multiplicando por 2 y a la vez aplicando la función módulo 9 a cada uno de los números de la cédula que están en posición impar, exceptuando a x, y luego sumándolos se obtiene: 1*2 + 0*2 + 2*2 + 3*2 + 2*x= 2 + 0 + 4 + 6 = 12
Sumando ahora el valor x, que ocupa la última posición impar, multiplicado por 2 y aplicando la función módulo 9, se obtiene:
12 + módulo(2*x,9)
Sumando ahora el valor x, que ocupa la última posición impar, multiplicado por 2 y aplicando la función módulo 9, se obtiene:
12 + módulo(2*x,9)
Luego sumando ahora los dígitos en posición par 1 + 0 + 9 + 4 = 14
Ahora sumando los dos resultados: 12 + módulo(2*x,9)+ 14 = 26 + módulo(2*x,9)
Primer método
Trabajando con la ecuación completa: 26 +módulo(2*x,9)
Nota: módulo(2*x,9) no es más que 2*x - 9 cuando 2*x ≥ 10
Segundo método
Trabajando con la suma de restos: resto(26) + resto(2*x módulo 9) o resto(2*x módulo 9) + resto(26)
Tercer método
Trabajando con el resto de la suma de restos : 10 - RESTO(resto(26) + resto(2*x módulo 9))
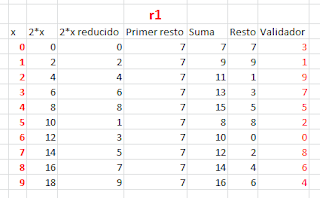
Pasos:
- Obtener el resto de 26 (que resulta de dividir entre 10). El resultado 6 colocarlo en la columna "Primer resto"
- Escribir la columna "x" con valores de 0 a 9.
- Obtener la columna 2*x
- Obtener la columna 2*x reducido, restando 9 a los valores de 2*x mayores o iguales a 10.
- Observar que la columna 2*x reducido es igual al resto de dividir entre 10, ya que todos son menores o iguales a 10.
- Hacer la suma de los dos restos y generar la columna suma
- Obtener la columna "Resto" que se obtiene del resto de dividir la columna suma ente 10.
- Obtener el validador con la siguiente operación: 10 - resto, tomando en cuenta que el validador es 0, cuando el resto es 0.
Videos:
Ejercicio 4_13
El Instituto Ecuatoriano de Seguridad Social IESS agenda citas considerando el último dígito (v), mientras que el Servicio de Rentas Internas SRI con el noveno (x).
¿Tienen los dígitos x, v la misma probabilidad de salir en ambos casos?
Recomendación o conducta de entrada
Practicar todos los ejercicios anteriores
El Instituto Ecuatoriano de Seguridad Social IESS agenda citas considerando el último dígito (v), mientras que el Servicio de Rentas Internas SRI con el noveno (x).
¿Tienen los dígitos x, v la misma probabilidad de salir en ambos casos?
Practicar todos los ejercicios anteriores
Solución:
Sea a b c d e f g h x v la cédula donde x es el noveno dígito, y, v el dígito validador.
Tomando los productos 2*a, 2*c, 2*e, 2*g de los dígitos en posición impar excluyendo a x
n1 = módulo(2*a,9) + módulo(2*c,9) +módulo(2*e,9) + módulo(2*g,9)
Entonces n1 es la suma de los productos de aplicar la función módulo a cada uno de dígitos que están en posición impar multiplicados por 2, excluyendo al dígito x.
n2 = b + d + f + h para los dígitos que están en posición par y finalmente
m = n1 + n2
Como m es un número natural se puede descomponer en m = n*10 + r1
Entonces la suma completa que permitirá obtener el validador (v) será:
m + 2*x = n*10 + r1+ 2*x.
De aquí en adelante se analizarán las diferentes casos de valores que vaya tomando la variable x, en la ecuación: n*10 + r1+ 2*x.
Para x = 0
Para x = 1
Para x = 2
Para x = 3
Para x = 4
Para x = 5
Para x = 6
Para x = 7
Para x = 8
Para x = 9
Prueba para r1 = 1
Prueba para r1 = 2
Prueba para r1 = 3
Prueba para r1 = 4
Prueba para r1 = 5
Prueba para r1 = 6
Prueba para r1 = 7
Prueba para r1 = 8
Prueba para r1 = 9
Un ejercicio adicional
Tome los ocho (8) primeros dígitos de su cédula y haga el siguiente ejercicio:
El primer resto se obtiene de dividir 26 entre 10 = 6, que se suma a 2*x reducido y a la cual se la divide entre 10 para obtener el siguiente resto y con ese dato obtener el validador.
¿Tienen los dígitos la misma probabilidad de salir en ambos casos?
Respuesta: ¿?
Ejercicio 4_14
Qué valores pueden tomar las variables x, y, z en la cédula siguiente:
1x0y2z3453
Recomendación o conducta de entrada
Practicar todos los ejercicios anteriores
Qué valores pueden tomar las variables x, y, z en la cédula siguiente:
1x0y2z3453
Recomendación o conducta de entrada
Practicar todos los ejercicios anteriores
Solución:
Tomar en cuenta que el validador es 3 y que las variables son ≤ 9
Obteniendo la suma:
2*1 + x + 2*0 + y + 2*2 + z + 2*3 + 4 + 2*5 =
2 + x + y + 4 + z + 6 + 4 + (10 - 9)=
17 + x + y + z (1) ecuación de la suma
a) Si, 23 < x + y + z ≤ 27, entonces 40 < 17 + x + y + z ≤ 44 por lo que el resto de dividir entre 10 es: 17 + x + y + z - 40 = x + y + z - 23 y el validador es: 10 -( x + y + z - 23) = 3 ==> - (x + y + z) + 33 = 3 ==> 30 = x + y + z, que no cumple porque 23 < x + y + z ≤ 27
b) Si, x + y + z = 23, entonces 17 + x + y + z = 40 y el validador sería 0, lo cual no es posible ya que, el validador, es 3.
c) Si, 13 < x + y + z < 23, entonces 30 < 17 + x + y + z < 40 por lo que el resto de dividir entre 10 es: 17 + x + y + z - 30 = x + y + z - 13 y el validador es: 10 -( x + y + z - 13) = 3 ==> - (x + y + z) + 23 = 3 ==> 20 = x + y + z, que no cumple porque 13 < x + y + z <23
d) Si, x + y + z = 13, entonces 17 + x + y + z = 30 y el validador sería 0, lo cual no es posible ya que, el validador, es 3.
e) Si, 3 < x + y + z < 13, entonces 20 < 17 + x + y + z < 30 por lo que el resto de dividir entre 10 es: 17 + x + y + z - 20 = x + y + z - 3 y el validador es: 10 -( x + y + z - 3) = 3 ==> - (x + y + z) + 13 = 3 ==> 10 = x + y + z, que sí cumple porque 3 < x + y + z < 13
Solución:
Las triadas que estén compuestas por naturales que satisfagan la ecuación del plano: x+y+z=10
algunos ejemplos
f) Si, x + y + z = 3, entonces 17 + x + y + z = 20 y el validador sería 0, lo cual no es posible ya que, el validador, es 3.
g) Si, 0 ≤ x + y + z < 3, entonces 17 ≤ 17 + x + y + z < 20 por lo que el resto de dividir entre 10 es: 17 + x + y + z - 10 = x + y + z + 7 y el validador es: 10 -( x + y + z + 7) = 3 ==> - (x + y + z) + 3 = 3 ==> 0 = x + y + z, que sí cumple porque 0 ≤ x + y + z < 3
Solución: x + y + z = 0 => x=0, y=0, z=0
Dada la función f siguiente:
A todos y cada uno de los subconjuntos a b c d e f g h x, de la cédula ecuatoriana: a b c d e f g h x v (donde x es un número entero mayor o igual a 0), se le asigna el valor v que es el validador de la cédula donde x está embebido.
Se pide:
Primero
Demostrar que la función f tiene dominio, conformado por 23.999.976 elementos
Segundo
Analizar si la probabilidad de conseguir cualquier entero verde es igual a la de conseguir su contraparte roja.
Primero
Demostrar que la función f tiene dominio, conformado por 23.999.976 elementos
Segundo
Analizar si la probabilidad de conseguir cualquier entero verde es igual a la de conseguir su contraparte roja.
Este ejercicio, por mí desarrollado, fue presentado en el evento realizado en Guayaquil Ecuador.
Así fue presentado en las redes sociales
"El maestro SuperCuy deja su impronta en el Coloquio Binacional de Matematicas ESPOL 2017 (Politécnica del Litoral Ecuador) con un problema que le llevó meses configurarlo.
Un abrazo y mis respetos a los profesores de matemáticas del mundo que estuvieron presentes,
Si requiere ayuda visite el blog, donde hay miles de problemas para ingreso a la Universidad: http://maestromate.blogspot.com/p/4-la-cedula-ecuatoriana.h… "
.
Un abrazo y mis respetos a los profesores de matemáticas del mundo que estuvieron presentes,
Si requiere ayuda visite el blog, donde hay miles de problemas para ingreso a la Universidad: http://maestromate.blogspot.com/p/4-la-cedula-ecuatoriana.h… "
.





































No hay comentarios:
Publicar un comentario